题目内容
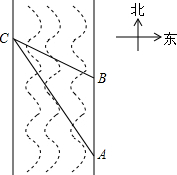 (2012•富宁县模拟)在一次数学活动课上,老师带领学生去测一条南北流向河流的河宽,如图所示,某学生在河东岸点A处观测河对岸水边点C,测得C在A北偏西30°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西60°的方向上.请你根据以上数据,帮助该同学计算出这条河的宽度.(精确到0.1,参考数据:
(2012•富宁县模拟)在一次数学活动课上,老师带领学生去测一条南北流向河流的河宽,如图所示,某学生在河东岸点A处观测河对岸水边点C,测得C在A北偏西30°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西60°的方向上.请你根据以上数据,帮助该同学计算出这条河的宽度.(精确到0.1,参考数据:| 2 |
| 3 |
分析:如图,过点C作CD⊥AB于D,由题意知道∠DAC=30°,∠DBC=60°,根据∠ACB=∠CBD-∠CAD=30°得到∠ACB=∠CAB,从而得到BC=AB=20米,然后在直角三角形CBD中利用解直角三角形求得CD的长即可;
解答: 解:如图,作CD⊥于AB于D
解:如图,作CD⊥于AB于D
由题意可知:AB=20米,∠CAD=30°,∠CBD=60°
∴∠ACB=∠CBD-∠CAD=30°
∴∠ACB=∠CAB
∴BC=AB=20米,
在Rt△CBD中,CD=CB•sin60°=20×
=10
≈17.3米,
答:这条河的宽度约为17.3米.
 解:如图,作CD⊥于AB于D
解:如图,作CD⊥于AB于D由题意可知:AB=20米,∠CAD=30°,∠CBD=60°
∴∠ACB=∠CBD-∠CAD=30°
∴∠ACB=∠CAB
∴BC=AB=20米,
在Rt△CBD中,CD=CB•sin60°=20×
| ||
| 2 |
| 3 |
答:这条河的宽度约为17.3米.
点评:此题主要考查了解直角三角形-方向角问题,解题时首先正确理解题意,然后根据题目隐含的数量关系列出方程解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
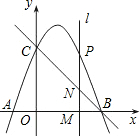 点,并与x轴交于另一点A.
点,并与x轴交于另一点A.