题目内容
设点P是正方形ABCD内任意一点,则PA+PB+PC+PD的最小值是
- A.边长的两倍
- B.周长
- C.两条对角线长之和
- D.以上都不对
C
分析:因为正方形ABCD的对称轴为AC与BD,所以只有当P在AC与BD的交点处时,PA+PB+PC+PD取得最小值.
解答:根据题意分析可得:正方形ABCD的对称轴为AC与BD;故当且仅当P在AC与BD的交点处时,PA+PB+PC+PD取得最小值,且其最小值为两条对角线长之和.故选C.
点评:本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
分析:因为正方形ABCD的对称轴为AC与BD,所以只有当P在AC与BD的交点处时,PA+PB+PC+PD取得最小值.
解答:根据题意分析可得:正方形ABCD的对称轴为AC与BD;故当且仅当P在AC与BD的交点处时,PA+PB+PC+PD取得最小值,且其最小值为两条对角线长之和.故选C.
点评:本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
相关题目
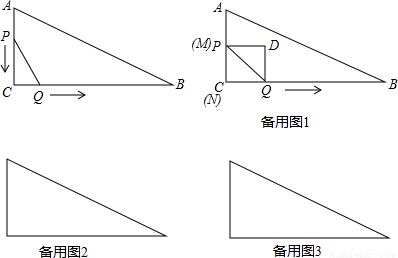
 (2009•保定二模)如图所示,Rt△ABC中,∠C=90°,AC=6,BC=12,点P从点A出发沿AC边向点C以每秒1个单位的速度移动,点Q从点C出发沿CB边向点B以每秒1个单位的速度移动,点P、Q同时出发,设移动时间为t秒(t>0).
(2009•保定二模)如图所示,Rt△ABC中,∠C=90°,AC=6,BC=12,点P从点A出发沿AC边向点C以每秒1个单位的速度移动,点Q从点C出发沿CB边向点B以每秒1个单位的速度移动,点P、Q同时出发,设移动时间为t秒(t>0). 如图,在平面直角坐标系xOy中,Rt△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知OA=4OB,AC=2BC=
如图,在平面直角坐标系xOy中,Rt△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知OA=4OB,AC=2BC= 如图,在矩形ABCD中,已知AB=1,BC=2,∠ABC的平分线交AD于点F,E为BC的中点,连接EF.
如图,在矩形ABCD中,已知AB=1,BC=2,∠ABC的平分线交AD于点F,E为BC的中点,连接EF.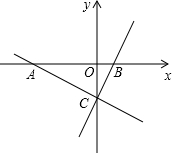 如图,在平面直角坐标系xOy中,Rt△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知OA=4OB,AC=2BC=
如图,在平面直角坐标系xOy中,Rt△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知OA=4OB,AC=2BC= .
.