ÌâÄ¿ÄÚÈİ
¡¾ÌâÄ¿¡¿Èçͼ£¬Ö±Ïß ![]() 1£ºy=kx+b ·Ö±ğ½» x Öá¡¢y ÖáÓÚµã B(4£¬0)¡¢N£¬Ö±Ïß
1£ºy=kx+b ·Ö±ğ½» x Öá¡¢y ÖáÓÚµã B(4£¬0)¡¢N£¬Ö±Ïß![]() 2:y=2x-1·Ö±ğ½» x Öá¡¢y ÖáÓÚµã M¡¢A£¬
2:y=2x-1·Ö±ğ½» x Öá¡¢y ÖáÓÚµã M¡¢A£¬![]() 1£¬
1£¬![]() 2 ½»µã P µÄ×ø±ê(m£¬2)£¬Çë¸ù¾İͼÏóËùÌṩµÄĞÅÏ¢½â´ğÏÂÁĞÎÊÌ⣺
2 ½»µã P µÄ×ø±ê(m£¬2)£¬Çë¸ù¾İͼÏóËùÌṩµÄĞÅÏ¢½â´ğÏÂÁĞÎÊÌ⣺

(1)µ± x ʱ£¬kx+b¡İ2x-1£»
(2)²»µÈʽ k![]() +b£¼0 µÄ½â¼¯ÊÇ £»
+b£¼0 µÄ½â¼¯ÊÇ £»
(3)ÔÚƽÃæÄÚÊÇ·ñ´æÔÚÒ»µã H£¬Ê¹µÃÒÔA£¬B£¬P£¬HËĵã×é³ÉµÄËıßĞÎÊÇƽĞĞËıßĞΣ®Èô´æÔÚ£¬Ö±½ÓĞ´³öµã H µÄ×ø±ê£¬Èô²»´æÔÚ£¬ËµÃ÷ÀíÓÉ£®
¡¾´ğ°¸¡¿(1)![]() £» (2)
£» (2)![]() £» (3)´æÔÚ£¬µãHµÄ×ø±êΪ(
£» (3)´æÔÚ£¬µãHµÄ×ø±êΪ(![]() £¬
£¬![]() )»ò(
)»ò(![]() £¬
£¬![]() )»ò(
)»ò(![]() £¬
£¬![]() )
)
¡¾½âÎö¡¿
(1)ÏÈÇóµÃµãPµÄ×ø±ê£¬¸ù¾İº¯ÊıͼÏ󣬼´¿ÉÇó½â£»
(2)¸ù¾İº¯ÊıͼÏ󣬼´¿ÉÇó½â£»
(3)ÉèµãHµÄ×ø±êΪ(a£¬n)£¬·ÖABΪ¶Ô½ÇÏß¡¢APΪ¶Ô½ÇÏß¼°BPΪ¶Ô½ÇÏßÈıÖÖÇé¿ö£¬ÀûÓÃƽĞĞËıßĞεÄĞÔÖÊ(¶Ô½ÇÏß»¥Ïàƽ·Ö)¿ÉÇó³öµãHµÄ×ø±ê£®
(1)¡ßµãP(m£¬2)ÔÚÖ±Ïß![]() 2:
2:![]() ÉÏ£¬
ÉÏ£¬
Áî![]() £¬Ôò
£¬Ôò![]() £¬
£¬
¡àµãPµÄ×ø±êΪ(![]() £¬2)£¬
£¬2)£¬
¹Û²ìº¯ÊıͼÏ󣬵±![]() ʱ£¬Ö±Ïß
ʱ£¬Ö±Ïß ![]() 1ÔÚÖ±Ïß
1ÔÚÖ±Ïß![]() 2µÄÉÏ·½£¬
2µÄÉÏ·½£¬
¡àµ±![]() ʱ£¬
ʱ£¬![]() £»
£»
(2)Ö±Ïß ![]() 1£º
1£º![]() ·Ö±ğ½»
·Ö±ğ½»![]() ÖáÓÚµã B(4£¬0)£¬
ÖáÓÚµã B(4£¬0)£¬
¹Û²ìº¯ÊıͼÏ󣬵±![]() ʱ£¬Ö±Ïß
ʱ£¬Ö±Ïß ![]() 1ÔÚ
1ÔÚ![]() ÖáµÄÏ·½£¬
ÖáµÄÏ·½£¬
¡à²»µÈʽ![]() µÄ½â¼¯Îª£º
µÄ½â¼¯Îª£º![]() £»
£»
(3)´æÔÚ£¬ÉèµãHµÄ×ø±êΪ(a£¬n)£¬
Áî![]() £¬Ôò
£¬Ôò![]() £¬
£¬
¡àµãAµÄ×ø±êΪ(0£¬![]() )£¬
)£¬
¡ßµãBµÄ×ø±êΪ(4£¬0)£¬µãPµÄ×ø±êΪ(![]() £¬2)£¬
£¬2)£¬
·ÖÈıÖÖÇé¿ö¿¼ÂÇ£¬ÈçͼËùʾ£º
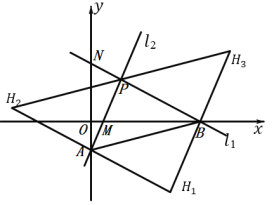
¢Ùµ±ABΪ¶Ô½ÇÏßʱ£¬
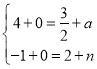
½âµÃ£º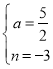 £¬
£¬
¡àµã![]() µÄ×ø±êΪ(
µÄ×ø±êΪ(![]() £¬
£¬![]() )£»
)£»
¢Úµ±APΪ¶Ô½ÇÏßʱ£¬
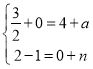 £¬
£¬
½âµÃ£º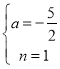 £¬
£¬
¡àµã![]() µÄ×ø±êΪ(
µÄ×ø±êΪ(![]() £¬
£¬![]() )£»
)£»
¢Ûµ±BPΪ¶Ô½ÇÏßʱ£¬
 £¬
£¬
½âµÃ£º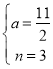 £¬
£¬
¡àµã![]() µÄ×ø±êΪ(
µÄ×ø±êΪ(![]() £¬
£¬![]() )£»
)£»
×ÛÉÏËùÊö£ºÔÚƽÃæÖ±½Ç×ø±êϵÖĞ´æÔÚµãH£¬Ê¹ÒÔµãA£¬B£¬P£¬HΪ¶¥µãµÄËıßĞÎÊÇƽĞĞËıßĞΣ¬µãHµÄ×ø±êΪ(![]() £¬
£¬![]() )»ò(
)»ò(![]() £¬
£¬![]() )»ò(
)»ò(![]() £¬
£¬![]() ) £®
) £®

 ¸ßÖбØË¢ÌâϵÁĞ´ğ°¸
¸ßÖбØË¢ÌâϵÁĞ´ğ°¸