题目内容
 如图,直线y1=2x+3和直线y2=-2x-1分别交y轴于点A,B,两直线交于点C.
如图,直线y1=2x+3和直线y2=-2x-1分别交y轴于点A,B,两直线交于点C.(1)求点C的坐标;
(2)求△ABC的面积.
考点:两条直线相交或平行问题
专题:
分析:(1)联立方程,解方程组即可求得C的坐标,
(2)根据点A、B的坐标求得AB的长度;由点C的横坐标的绝对值即为该三角形的高;
(2)根据点A、B的坐标求得AB的长度;由点C的横坐标的绝对值即为该三角形的高;
解答:解:(1)∵
,
解得
.
∴C的坐标为(-1,1);
(2))∵y1=2x+3与y轴的交点A(0,3),直线y2=-2x-1与y轴的交点B(0,-1).
∴AB=4.
又∵C(-1,1).
∴△ABC的面积=
×4×1=2;
|
解得
|
∴C的坐标为(-1,1);
(2))∵y1=2x+3与y轴的交点A(0,3),直线y2=-2x-1与y轴的交点B(0,-1).
∴AB=4.
又∵C(-1,1).
∴△ABC的面积=
| 1 |
| 2 |
点评:本题考查了两条直线相交或平行问题、待定系数法以及三角形的面积.注意“数形结合”数学思想的应用.

练习册系列答案
相关题目
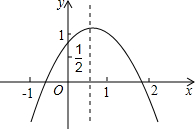 抛物线y=ax2+bx+c的图象如图所示,下列结论正确的是( )
抛物线y=ax2+bx+c的图象如图所示,下列结论正确的是( )| A、abc>0 |
| B、a+c>0 |
| C、b2+4a>4ac |
| D、2a+b>0 |
 根据图中的程序,当输入x=5时,输出的结果y=
根据图中的程序,当输入x=5时,输出的结果y=