Question

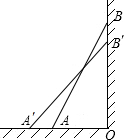如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为7m，梯子的顶端B到地面的距离为24m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于15m．同时梯子的顶端B下降至B′，那么BB′等于（　　）

A．3m

B．4m

C．5m

D．6m

Answer 1

分析：由题意可知OA=7，OB=24，先利用勾股定理求出AB，梯子移动过程中长短不变，所以AB=A′B′，又由题意可知OA′=15，利用勾股定理分别求OB′长，把其相减得解．

解答：解：在直角三角形AOB中，因为AO=7，OB=24
由勾股定理得：AB=

AO2+BO2

=25m，
由题意可知AB=A′B′，
又OA′=15m，根据勾股定理得：OB′=

A′B′2-A′O2

=20m，
∴BB′=BO-B′O=24-20=4米．
故选B．

点评：本题考查了勾股定理的应用，解题时注意勾股定理应用的环境是在直角三角形中．