题目内容
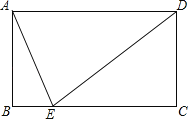
【题目】如图是某斜拉桥引申出的部分平面图，AE，CD是两条拉索，其中拉索CD与水平桥面BE的夹角为72°，其底端与立柱AB底端的距离BD为4米，两条拉索顶端距离AC为2米，若要使拉索AE与水平桥面的夹角为35°，请计算拉索AE的长．（结果精确到0.1米）（参考数据：sin35°≈
，cos35°≈
，tan35°≈
，sin72°≈
，cos72°≈
，tan72°≈
）
【答案】拉索AE的长为26.2m．
【解析】
利用锐角三角函数关系得出AB的长，进而得出AE的长即可得出答案．
解：由题意可得：tan72°=
=
=
，
解得：BC=
，
则AB=BC+AC=+2＝
（m），
故sin35°=
=
=
，
解得：AE≈26.2，
答：拉索AE的长为26.2m．
【题目】某校开展主题为“垃圾分类，绿色生活新时尚”的宣传活动，为了解学生对垃圾分类知识的掌握情况，学生会随机抽取了20名七、八年级学生（每个年级各10人）进行问卷调查，并把他们的得分绘制成了如下表格，计分采用10分制（得分均取整数）成绩达到6分或6分以上为及格，达到9分及以上为优秀，成绩如表1所示，并制作了成绩分析表（表2）．
表1
七年级 | 5 | 8 | 8 |
| 8 | 10 | 10 | 8 | 5 | 5 |
八年级 | 10 | 6 | 6 | 9 |
| 4 | 5 | 7 | 10 | 8 |
表2
年级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
七年级 | 7.6 | 8 | 8 | 3.82 | 70% |
|
八年级 | 7.5 |
| 10 | 4.94 | 80% | 40% |
（1）在表1中，
_____，
_____；在表2中，
_____，
______；
（2）根据表2成绩数据分析，你认为哪个年级的学生对垃圾分类了解更加深入，请说明你的理由；
（3）小明根据表2数据作出如下判断：
①七年级学生成绩的平均数高于八年级，故七年级学生一定比八年级学生优秀；
②被调查对象中，七年级学生的成绩更加稳定；
③学校七年级和八年级共有400人，估计有280人成绩达到优秀；
④七年级不及格人数比八年级多；
对小明的四个结论，随机任选两个，求都是错误的概率．
