题目内容
19. 一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )
一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )| A. | 甲、乙两地的距离为420km | B. | y1=60x,y2=$\left\{\begin{array}{l}{90x}\\{100x-230}\end{array}\right.$ | ||
| C. | 货车出发4.5h与小轿车首次相遇 | D. | 两车首次相遇时距乙地150km |
分析 A、观察函数图象,即可找出甲乙两地的距离,选项A正确;B、观察函数图象,找出点的坐标,利用待定系数法即可求出两函数解析式,选项B错误;C、将y=270代入y1=60x中求出x值,选项C正确;D、由两车首次相遇的时间即可求出两车首次相遇时距乙地的距离,选项D正确.此题得解.
解答 解:A、由图象可得,甲乙两地的距离是420km,
∴选项A正确;
B、设货车的路程y1与x的函数关系式为y1=kx,小轿车的路程y2与x的函数关系式为y2=mx+n,
将(7,420)代入y1=kx中,
420=7k,解得:k=60,
∴货车的路程y1与x的函数关系式为y1=60x;
当x=5.75时,y1=60x=60×5.75=345,
将(5.75,345)、(6.5,420)代入y2=mx+n中,
$\left\{\begin{array}{l}{5.75m+n=345}\\{6.5m+n=420}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=100}\\{n=-230}\end{array}\right.$,
∴y2=100x-230(5≤x≤6.5).
当x=5.5时,y2=100x-230=100×5-230=270,
将(0,0)、(3,270)代入y2=mx+n中,
$\left\{\begin{array}{l}{n=0}\\{3m+n=270}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=90}\\{n=0}\end{array}\right.$,
∴y2=90x(0≤x≤3).
∴y2=$\left\{\begin{array}{l}{90x(0≤x≤3)}\\{270(3≤x≤5)}\\{100x-230(5≤x≤6.5)}\end{array}\right.$,
∴选项B错误;
C、令y1=60x=270,解得:x=4.5,
∴货车出发4.5h与小轿车首次相遇,选项C正确;
D、∵货车出发4.5h与小轿车首次相遇,
∴y1=60x=60×4.5=270,
∴420-270=150(km),
∴两车首次相遇时距乙地150km,选项D正确.
故选B.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及一次函数图象,逐一分析四个选项的正误是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,该几何体的俯视图是( )
如图所示,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
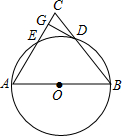 如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,交AC于F,DG⊥AC于G.
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于D,交AC于F,DG⊥AC于G.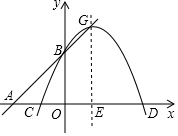 已知二次函数y=ax2-4ax+a2+2(a<0)图象的顶点G在直线AB上,其中
已知二次函数y=ax2-4ax+a2+2(a<0)图象的顶点G在直线AB上,其中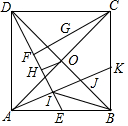 如图,正方形ABCD的边长为2,对角线AC与BC相交于O,E为AB的中点,F为DE的中点,G为CF的中点,OH⊥DE于H,过A作AI⊥DE于I,交BD于J,交BC于K,连接BI,下列结论:①G到AC的距离等于$\frac{\sqrt{2}}{8}$;②OH=$\frac{\sqrt{5}}{5}$;③BK=$\frac{1}{2}$AK;④∠BIJ=45°.其中正确的结论是( )
如图,正方形ABCD的边长为2,对角线AC与BC相交于O,E为AB的中点,F为DE的中点,G为CF的中点,OH⊥DE于H,过A作AI⊥DE于I,交BD于J,交BC于K,连接BI,下列结论:①G到AC的距离等于$\frac{\sqrt{2}}{8}$;②OH=$\frac{\sqrt{5}}{5}$;③BK=$\frac{1}{2}$AK;④∠BIJ=45°.其中正确的结论是( )