题目内容
如图中的虚线网格我们称为正三角形网格,它的每一个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.
(1)图①中,已知四边形ABCD是平行四边形,求△ABC的面积和对角线AC的长;
(2)图②中,求四边形EFGH的面积.

(1)图①中,已知四边形ABCD是平行四边形,求△ABC的面积和对角线AC的长;
(2)图②中,求四边形EFGH的面积.

分析:(1)首先过点A作AK⊥BC于K,由每一个小三角形都是边长为1个单位长度的正三角形,可求得该小正三角形的高为
,则可求得△ABC的面积,然后由勾股定理求得对角线AC的长;
(2)首先过点E作ET⊥FH于T,即可得四边形EFGH的面积为:2S△EFH=2×
×ET×FH.
| ||
| 2 |
(2)首先过点E作ET⊥FH于T,即可得四边形EFGH的面积为:2S△EFH=2×
| 1 |
| 2 |
解答:解: (1)由图①,过点A作AK⊥BC于K,
(1)由图①,过点A作AK⊥BC于K,
∵每一个小三角形都是边长为1个单位长度的正三角形.
∴该小正三角形的高为
,
则:S△ABC=
×AK×CB=
×3×
×CB=
;
∵AK=
,BK=
,
∴KC=
,
故由勾股定理可求得:AC=
.
(2)由图②,过点E作ET⊥FH于T,
又由题意可知:四边形EFGH的面积为:2S△EFH=2×
×ET×FH=ET×FH=2×
×6=6
.
 (1)由图①,过点A作AK⊥BC于K,
(1)由图①,过点A作AK⊥BC于K,∵每一个小三角形都是边长为1个单位长度的正三角形.
∴该小正三角形的高为
| ||
| 2 |
则:S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
15
| ||
| 4 |
∵AK=
3
| ||
| 2 |
| 3 |
| 2 |
∴KC=
| 7 |
| 2 |
故由勾股定理可求得:AC=
| 19 |
(2)由图②,过点E作ET⊥FH于T,
又由题意可知:四边形EFGH的面积为:2S△EFH=2×
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:此题考查了平行四边形的性质以及等边三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
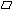 ABCD含有多少个单位正三角形?
ABCD含有多少个单位正三角形?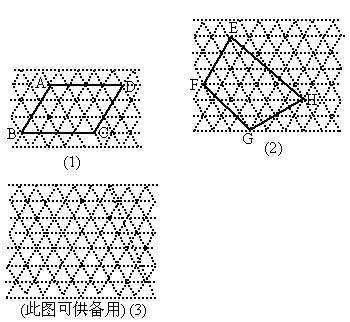
 ABCD含有多少个单位正三角形?
ABCD含有多少个单位正三角形?

