题目内容
3.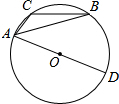 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是4,sinB=$\frac{1}{4}$,则线段AC的长为2.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是4,sinB=$\frac{1}{4}$,则线段AC的长为2.
分析 连结CD如图,根据圆周角定理得到∠ACD=90°,∠D=∠B,则sinD=sinB=$\frac{1}{4}$,然后在Rt△ACD中利用∠D的正弦可计算出AC的长.
解答 解:连结CD,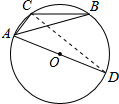 如图,
如图,
∵AD是⊙O的直径,
∴∠ACD=90°,
∵∠D=∠B,
∴sinD=sinB=$\frac{1}{4}$,
在Rt△ACD中,∵sinD=$\frac{AC}{AD}$=$\frac{1}{4}$,
∴AC=$\frac{1}{4}$AD=$\frac{1}{4}$×8=2.
故答案为2.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了解直角三角形.

练习册系列答案
相关题目
11.下列计算结果正确的是( )
| A. | 2a3+a3=3a6 | B. | (-a)2•a3=-a6 | C. | (-$\frac{1}{2}$)-2=4 | D. | (-2)0=-1 |
12.三角形三条中线的交点叫做三角形的( )
| A. | 内心 | B. | 外心 | C. | 中心 | D. | 重心 |
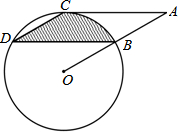 如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π)
如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,BD=4$\sqrt{3}$,则由弦CD,BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π.(结果保留π) 我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA 如图是由6个相同的小立方块搭成的几何体,这个几何体的左视图是( )
如图是由6个相同的小立方块搭成的几何体,这个几何体的左视图是( )


