题目内容
13.先化简再求值:($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)÷$\frac{{x}^{2}-16}{{x}^{2}+4x}$,其中x=2-$\sqrt{2}$.分析 先根据分式混合运算的法则把原式进行化简,代入计算即可.
解答 解:原式=$[\frac{x+2}{x(x-2)}-\frac{x-1}{(x-2)^{2}}]÷\frac{(x+4)(x-4)}{x(x+4)}$
=$\frac{(x+2)(x-2)-x(x-1)}{x(x-2)^{2}}•\frac{x}{x-4}$
=$\frac{1}{(x-2)^{2}}$;
当x=2-$\sqrt{2}$时,原式=$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
18.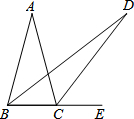 如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
 如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )| A. | 15° | B. | 17.5° | C. | 20° | D. | 22.5° |
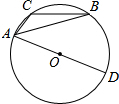
2. 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是( )| A. | 60° | B. | 90° | C. | 100° | D. | 120° |
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是4,sinB=$\frac{1}{4}$,则线段AC的长为2.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是4,sinB=$\frac{1}{4}$,则线段AC的长为2.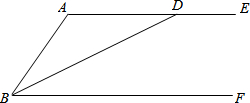 如图,已知BD平分∠ABF,且交AE于点D,
如图,已知BD平分∠ABF,且交AE于点D, 甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.