题目内容
若等边三角形ABC的边长为2
cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是
| 3 |
相切
相切
.分析:求得等边三角形的高后与半径3比较即可确定直线与圆的位置关系.
解答:解:∵等边三角形ABC的边长为2
cm,
∴等边三角形的高为:
=3
∵以3cm为半径作⊙A,
∴BC所在直线与⊙A的位置关系是相切,
故答案为:相切.
| 3 |
∴等边三角形的高为:
(2
|
∵以3cm为半径作⊙A,
∴BC所在直线与⊙A的位置关系是相切,
故答案为:相切.
点评:考查了直线和圆的位置关系与数量之间的联系.能够综合运用等腰三角形的性质和勾股定理求解.

练习册系列答案
相关题目
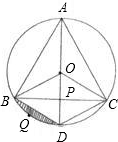 等边三角形ABC内接于⊙0,连接OA,OB,OC,延长AO分别交BC于点P,
等边三角形ABC内接于⊙0,连接OA,OB,OC,延长AO分别交BC于点P,
 BC,垂足为F
BC,垂足为F