题目内容
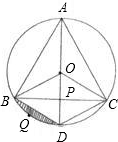 等边三角形ABC内接于⊙0,连接OA,OB,OC,延长AO分别交BC于点P,
等边三角形ABC内接于⊙0,连接OA,OB,OC,延长AO分别交BC于点P, |
| BC |
(1)判断四边形BDCO是哪一种特殊四边形,并说明理由;
(2)若等边三角形ABC的边长6
| 3 |
(3)在劣弧
 |
| BD |
分析:(1)可先由四边形各角的大小求出各边之间的关系,然后即可判断四边形BDCO为何种特殊四边形;
(2)先由菱形性质求出BP的长,再由等边三角形性质及求出∠POB的角度,然后即可由三角形边角关系求出OB的长,即⊙0的半径;
(3)弓形BQD的面积可由求扇形OBD与三角形OBD之差间接求得.
(2)先由菱形性质求出BP的长,再由等边三角形性质及求出∠POB的角度,然后即可由三角形边角关系求出OB的长,即⊙0的半径;
(3)弓形BQD的面积可由求扇形OBD与三角形OBD之差间接求得.
解答:解:(1)四边形BDCO是菱形理由如下:
∵AB=BC=AC,
∴∠AOB=∠BOC=∠COA=120°,
∴∠BOD=180°-∠AOB=60°,
∴∠COD=180°-∠AOC=60°;
又∵OB=OD,
∴△OBD为正三角形,
∴OB=OD=BD
同理可得OC=CD,
∴OB=OC=BO=CD即四边形BDCO是菱形;(3分)
(2)由菱形性质可知,BP=
BC=
×6
=3
;
∵△ABC为等边三角形,∠PBO=30°,OP=3,BO=6,
∴⊙O的半径OB为6.(3分)
(3)S弓形BQD=S扇形-S△BOD=
-
×62=6π-9
.(2分)
∵AB=BC=AC,
∴∠AOB=∠BOC=∠COA=120°,
∴∠BOD=180°-∠AOB=60°,
∴∠COD=180°-∠AOC=60°;
又∵OB=OD,
∴△OBD为正三角形,
∴OB=OD=BD
同理可得OC=CD,
∴OB=OC=BO=CD即四边形BDCO是菱形;(3分)
(2)由菱形性质可知,BP=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵△ABC为等边三角形,∠PBO=30°,OP=3,BO=6,
∴⊙O的半径OB为6.(3分)
(3)S弓形BQD=S扇形-S△BOD=
| 60π×62 |
| 360 |
| ||
| 4 |
| 3 |
点评:本题考查了正三角形与圆,正三角形的性质,菱形的性质与判定及面积求法,具有较强的综合性.

练习册系列答案
相关题目
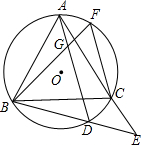 如图,等边三角形ABC内接于⊙O,D为
如图,等边三角形ABC内接于⊙O,D为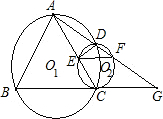 如图,已知等边三角形△ABC内接于⊙O1,⊙O2与BC相切于C,与AC相交于E,与⊙O1相交于另一点D,直线AD交⊙O2于另一点F,交BC的延长线于G,点F为AG的中点.对于如下四个结论:①EF∥BC;②BC=FC;③DE•AG=AB•EC;④弧AD=弧DC.其中一定成立的是( )
如图,已知等边三角形△ABC内接于⊙O1,⊙O2与BC相切于C,与AC相交于E,与⊙O1相交于另一点D,直线AD交⊙O2于另一点F,交BC的延长线于G,点F为AG的中点.对于如下四个结论:①EF∥BC;②BC=FC;③DE•AG=AB•EC;④弧AD=弧DC.其中一定成立的是( ) 4、如图,等边三角形ABC内接于⊙O,连接OB,OC,那么∠BOC的度数是( )
4、如图,等边三角形ABC内接于⊙O,连接OB,OC,那么∠BOC的度数是( ) 如图,等边三角形ABC内接于⊙O,连接OA,OB,OC,延长AO,分别交BC于点P,与⊙O交于点D,连接BD,CD.那么:①四边形BDCO是菱形,②若⊙O的半径为r,三角形的边长为
如图,等边三角形ABC内接于⊙O,连接OA,OB,OC,延长AO,分别交BC于点P,与⊙O交于点D,连接BD,CD.那么:①四边形BDCO是菱形,②若⊙O的半径为r,三角形的边长为 如图,边长为2
如图,边长为2