题目内容
若等边三角形ABC的边长为a,且三角形内一点P到各边的距离分别是ha,hb,hc,则ha+hb+hc=分析:本题考查的是等边三角形的性质.分别连接PA、PB、PC将△ABC分成3个小三角形,再根据等边△ABC的面积等于三个小三角形的面积之和,就可以得出答案.
解答:解:设△ABC的为h,根据等边三角形的性质h=
a,
分别链结PA,PB,PC,将△ABC分割成△APB、△APC、△BPC
S△ABC=S△APB+S△APC+S△BPC=a•(ha+hb+hc)•
=
ah
那么,ha+hb+hc=
a
| ||
| 2 |
分别链结PA,PB,PC,将△ABC分割成△APB、△APC、△BPC
S△ABC=S△APB+S△APC+S△BPC=a•(ha+hb+hc)•
| 1 |
| 2 |
| 1 |
| 2 |
那么,ha+hb+hc=
| ||
| 2 |
点评:本题考查了等边三角形高为底边长的
倍的性质.
| ||
| 2 |

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
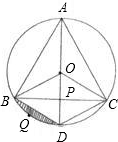 等边三角形ABC内接于⊙0,连接OA,OB,OC,延长AO分别交BC于点P,
等边三角形ABC内接于⊙0,连接OA,OB,OC,延长AO分别交BC于点P,
 BC,垂足为F
BC,垂足为F