Question

【题目】如图，在△ABC中，AB＝AC，P是边BC的中点，PD⊥AB，PE⊥AC，垂足分别为D、E

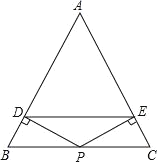
（1）求证：PD＝PE；

（2）DE与BC平行吗？请说明理由；

（3）请添加一个条件，使四边形ADPE为正方形，并加以证明．

Answer 1

【答案】（1）见解析；（2）DE∥BC，理由见解析；（3）当∠A＝90°时，使四边形ADPE为正方形

【解析】

（1）由已知条件，利用角角边可证△PDB≌△PEC，所以PD＝PE;

（2）由（1）中△PDB≌△PEC可得BD=CE，结合条件AB=AC，利用平行线分线段成比例的逆定理可得出DE∥BC.

（3）∠A=90°时，易得四边形ADPE为矩形，由邻边AD=AE可得 四边形ADPE为正方形.

（1）证明：∵AB＝AC，

∴∠B＝∠C，

∵PD⊥AB，PE⊥AC，

∴∠PDB＝∠PEC＝90°，

∵P是BC的中点，

∴BP＝PC，

即∠BDP＝∠PEC＝90°，∠B＝∠C，PB＝PC，

∴△PDB≌△PEC（AAS），

∴PD＝PE．

（2）答：DE∥BC，

理由是：∵△PDB≌△PEC，

∴BD＝CE，

∵AB＝AC，

∴＝，

∴DE∥BC．

（3）答：当∠A＝90°时，使四边形ADPE为正方形，

证明：∵∠A＝∠ADP＝∠AEP＝90°，

∴四边形ADPE是矩形，

∵AB＝AC，BD＝CE，

∴AD＝AE，

∴矩形ADPE是正方形，

即当∠A＝90°时，使四边形ADPE为正方形．