Question

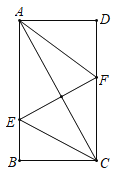
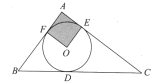
【题目】如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB＝5，BC＝13，CA＝12，则阴影部分(即四边形AEOF)的面积是( )

A.4B.6.25C.7.5D.9

Answer 1

【答案】A

【解析】

先利用勾股定理判断△ABC为直角三角形，且∠BAC=90°，继而证明四边形AEOF为正方形，设⊙O的半径为r，利用面积法求出r的值即可求得答案.

∵AB=5，BC=13，CA=12，

∴AB2+AC2=BC2，

∴△ABC为直角三角形，且∠BAC=90°，

∵⊙O为△ABC内切圆，

∴∠AFO=∠AEO=90°，且AE=AF，

∴四边形AEOF为正方形，

设⊙O的半径为r，

∴OE=OF=r，

∴S四边形AEOF=r，

连接AO，BO，CO，

∴S△ABC=S△AOB+S△AOC+S△BOC，

∴，

∴r=2，

∴S四边形AEOF=r=4，

故选A.