题目内容
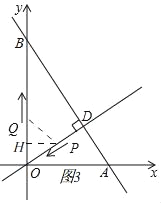
【题目】如图,在平面直角坐标系中,O为坐标原点,已知直线y=﹣![]() x+8与x轴、y轴分别交于A、B两点.直线OD⊥直线AB于点D.现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止.设运动时间为t秒.
x+8与x轴、y轴分别交于A、B两点.直线OD⊥直线AB于点D.现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止.设运动时间为t秒.
(1)点A的坐标为_____;线段OD的长为_____.
(2)设△OPQ的面积为S,求S与t之间的函数关系(不要求写出取值范围),并确定t为何值时S的值最大?
(3)是否存在某一时刻t,使得△OPQ为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.

【答案】(1)(6,0), ![]() ; (2)
; (2) ![]() ,当
,当![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() ;(3)
;(3) ![]() 为等腰三角形时,t的值为
为等腰三角形时,t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】试题分析:
试题解析:(1)![]() 与x轴、y轴分别交于A、B两点,
与x轴、y轴分别交于A、B两点,
令x=0,则y=8,
∴![]()
∴![]()
令y=0,则![]()
∴![]() ∴
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
故答案为: ![]()
![]()
(2)如图1,
在![]() 中,
中, ![]()
根据勾股定理得,span> ![]()
∴![]()
由运动知, ![]()
∴![]()
过点P作![]() 于H,
于H,
在![]() 中,
中, ![]()
∴![]()
∴![]()
![]()
∴当![]() 时,S最大
时,S最大![]()
(3)∵![]() 为等腰三角形,
为等腰三角形,
∴①当![]() 时,
时,
∴![]()
∴![]()
②当OQ=PQ时,在![]() 中,
中, ![]()
如图2,过点Q作![]() 于M,
于M,
∴![]()
在![]() 中,
中, ![]()
∴![]()
∴![]()
③当![]() 时,如图3,
时,如图3,
过点P作![]() 于H,
于H,
∴![]()
在![]() 中,
中, ![]()
∴![]()
∴![]()
∴![]() 为等腰三角形时,t的值为
为等腰三角形时,t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.



练习册系列答案
相关题目