题目内容
图中各图是在同一直角坐标系内，二次函数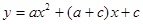
与一次函数
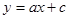的大致图象，有且只有一个是正确的，正确的是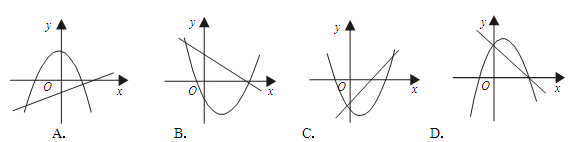
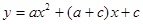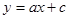与一次函数的大致图象，有且只有一个是正确的，正确的是D
试题分析：本题可先由一次函数
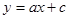图象得到字母系数的正负，再与二次函数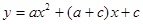的图象相比较看是否一致，用排除法即可解答．A、一次函数
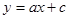的图象过一、三象限，a＞0，与二次函数开口向下，即a＜0相矛盾，错误；B、一次函数
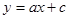的图象过二、四象限，a＜0，与二次函数开口向上，a＞0相矛盾，错误；C、
，故此二次函数与x轴的两个交点为（
，0），（-1，0），一次函数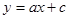与x轴的交点为（，0），故两函数在x轴上有交点，错误；排除A、B、C，故选D．
点评：此类问题是初中数学的重点，是中考常见题，一般难度不大，需熟练掌握.
练习册系列答案
相关题目
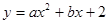的图象与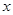
轴交于A（－3，0），B（1，0）两点，与y轴交于点C．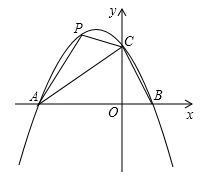
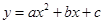的图象与
轴交于（– 1，0），（3，0）；下列说法正确的是（ ）
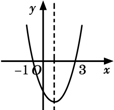
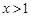时，y随x值的增大而增大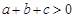
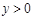时，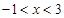
（米）与水平距离
（米）满足关系式为：
，则小林这次铅球推出的距离是 米．
x2－
x与x轴交于O，A两点. 半径为1的动圆（⊙P），圆心从O点出发沿抛物线向靠近点A的方向移动；半径为2的动圆（⊙Q），圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发，且移动速度相等，当运动到P，Q两点重合时同时停止运动. 设点P的横坐标为t .