��Ŀ����
��һ��������ƽ������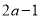 ��
��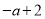 ����
����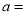 _______�����������___
_______�����������___
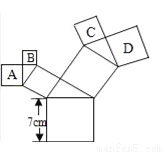
��ͼ�����е��ı��ζ��������Σ����е������ζ���ֱ�������Σ��������������εı߳�Ϊ7cm����������A��B��C��D�����֮��Ϊ______cm2��
����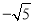 ����
����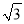 ������������__��
������������__��
���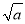 ��ƽ��������
��ƽ��������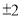 ����ô
����ô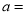 ______.
______.
9��ƽ������_______
�鿴����֪����ͼ��һ�ִ���16����/ʱ���ٶȴӸۿ�A�����������У���һ�ִ���12����/ʱ���ٶ�ͬʱ�Ӹۿ�A�������Ϸ����У��뿪�ۿ�2Сʱ��,���������( )
A��25���� B��30���� C��35���� D��40����
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
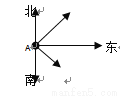
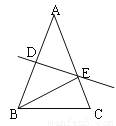
��ͼ����E��F��BC�ϣ�BE=CF����A=��D����B=��C��AF��DE���ڵ�O��
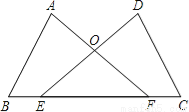
��1����֤��AB=DC��
��2�����жϡ�OEF����״����˵�����ɣ�
��1��֤������BE=CF�� ��BE+EF=CF+EF�� ��BF=CE�� �֡ߡ�A=��D����B=��C�� ���ABF�ա�DCE��AAS���� ��AB=DC�� ��2���������� ��OEFΪ���������� �������£��ߡ�ABF�ա�DCE�� ���AFB=��DEC�� ��OE=OF�� ���OEFΪ���������Σ� �������������������1������BE=CF�õ�...��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��A��2��3����B��3��1����C����2����2�������ڸ���ϣ�
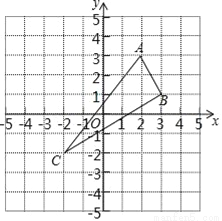
��1��������ABC����y��ԳƵġ�A1B1C1��
��2��ֱ��д����ABC����x��ԳƵġ�A2B2C2�ĸ������ꣻ
��3�������ABC�������
�鿴���Ȼ�������ֵ�� 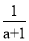 ��
��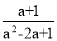 ��
��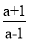 ������a=
������a=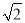 .
.
��1������4��x+1��2����2x��5����2x+5����
��2���ⷽ�̣� 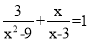 ��
��
��ͼ����ABC�У�AB=AC=13cm��AB�Ĵ�ֱƽ���߽�AB��D,��AC��E,����EBC���ܳ�Ϊ21cm,��BC= cm��
�������ⲻ��ȵ�����ʵ��a��b���������㡰*�������£� 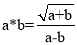 ����
����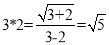 ,��ô8*12=_______.
,��ô8*12=_______.
- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���и�ʽ�У�������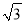 �ϲ����� ( )
�ϲ����� ( )
A. 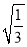 B.
B. 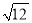 C.
C. 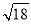 D.
D. 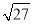
��x2��kxy+9y2��һ����ȫƽ��ʽ����k��ֵΪ��������
A. 3 B. ��6 C. 6 D. +3
�鿴������������ȷ���ǣ�������
A. 3x2+2x3=5x5 B. ����3.14��0=0 C. 3��2=��6 D. ��x3��2=x6
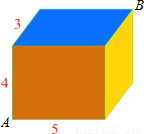
�鿴����ͼ��ʾ����һ�������壬���ij��������߷ֱ�Ϊ5cm��3cm��4cm���ڶ���A����һֻ���ϣ�����Ե��붥��A��ԵĶ���B��ʳ�
��1���뻭���������س�����������е�������·ͼ����ƽ��չ��ͼ����
��2����֪�����س�����������е��ٶ���1cm/s���������ܷ���8���ڻ�ȡ��ʳ�
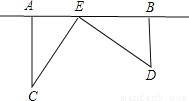
Ϊ�˷ḻ�����ͯ��ҵ�����ij����Ҫ����ͼ��ʾAB���ڵ�ֱ�߽�һͼ���ң�������������ѧУ���ڵ�λ���ڵ�C�͵�D����CA��AB��A��DB��AB��B����֪AB��25km��CA��15km��DB��10km�����ʣ�ͼ����EӦ�ý��ھ��A����km��������ʹ��������ѧУ�ľ������?
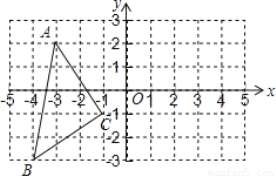
��ͼ������Ҫ��ش��������⣺
��1����A����y��ԳƵ�A�����������������B����y��ԳƵ�B�������������
��2��������ABC����y��ԳƵ�ͼ�Ρ�A��B��C�䣨��Ҫ��д������
��3�����ABC�������
- ���ͣ���ѡ��
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
�������ϻ�����ʾ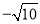 �ĵ㣮
�ĵ㣮
����д������������ͼ�ۼ���
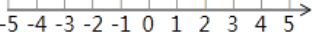
����
��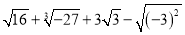
��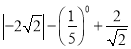
��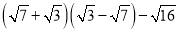
��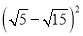
��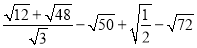
��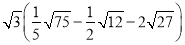
һ��ֱ�������ε�б�߳���һֱ�DZ߳���2����һֱ�DZ߳�Ϊ6����ֱ�������ε�б�߳�Ϊ____
�鿴������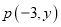 ����ƽ��3����λ���ȣ�����ƽ��2����λ���Ⱥ�õ���Q(x����1)����
����ƽ��3����λ���ȣ�����ƽ��2����λ���Ⱥ�õ���Q(x����1)����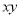 ��__________.
��__________.
����֪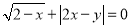 ����ô
����ô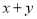 ��ֵΪ ___________
��ֵΪ ___________
��һ��������ƽ������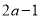 ��
��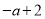 ����
����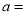 _______�����������___
_______�����������___
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��֪����ͼ��һ�ִ���16����/ʱ���ٶȴӸۿ�A�����������У���һ�ִ���12����/ʱ���ٶ�ͬʱ�Ӹۿ�A�������Ϸ����У��뿪�ۿ�2Сʱ��,���������( )

A��25���� B��30���� C��35���� D��40����
D �������� ������������ݷ�λ�ǿ�֪�������ߵķ������ù�����ֱ�ǣ�Ȼ�����·��=�ٶȡ�ʱ�䣬���������ֱ�����32��24���ٸ��ݹ��ɶ������������������֮��ľ��룮 ��������ʻ�ķ����Ƕ�������Ͷ��Ϸ��� ���BAC=90�㣬 ��Сʱ�����Ҵ��ֱ���ʻ��16��2=32��12��2=24��� ���ݹ��ɶ����ã�������� ��ѡD.��ͼ����������OABC����ƽ��ֱ������ϵ�У�O��ԭ�㣬A������Ϊ��1�� 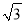 �������C������Ϊ�� ��
�������C�������� ��
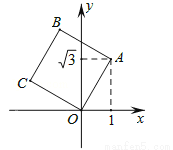
A. ����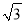 ��1�� B. ����1��
��1�� B. ����1�� 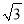 �� C. ��
�� C. ��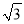 ��1�� D. ����
��1�� D. ����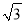 ����1��
����1��
��Rt��ABC�У���C��90�㣬��A, ��B, ��C���Եı߷ֱ�Ϊa��b��c, ��֪a��b��3��4��c��10�����ABC�����Ϊ( )
A. 24 B. 12 C. 28 D. 30
�鿴��.��ͼ���ȱߡ�ABC�߳�Ϊ3cm������ABC��AC����ƽ��1cm���õ���DEF�����ı���ABEF���ܳ�( )
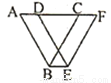
A. 9cm B. 10cm C. 11cm D. 12cm
�鿴����M����3����5������N������ƽ��4����λ��������ƽ��3����λ���õ������N������Ϊ�� ��
A����0����9�� B������6����1�� C����1����2�� D����1����8��
�鿴��������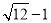 �Ĵ�С��������������֮�䣨������
�Ĵ�С��������������֮�䣨������
A. 1��2 B. 2��3 C. 3��4 D. 4��5
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
����ʽ����ȷ���ǣ�������
A. 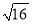 =��4 B. ��
=��4 B. ��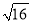 =4 C.
=4 C. 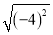 =-4 D. ��
=-4 D. ��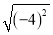 =��4
=��4
���ж��θ�ʽ�е������θ�ʽ�� �� ��
A. 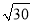 B.
B. 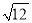 C.
C. 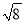 D.
D. 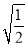
��ʵ��0.333����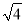 ��
�� 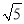 ��-�У�3.1415��2.010010001������������1֮��0�ĸ��������ӣ��У��������У�������
��-�У�3.1415��2.010010001������������1֮��0�ĸ��������ӣ��У��������У�������
A. 1�� B. 2�� C. 3�� D. 4��
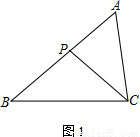
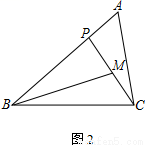
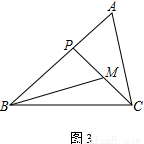
�鿴���ڡ�ABC�У�PΪ��AB��һ�㣮
��1����ͼ1������ACP����B����֤��AC2��AP��AB��
��2����MΪCP���е㣬AC��2��
�� ��ͼ2������PBM����ACP��AB��3����BP�ij���
�� ��ͼ3������ABC��45�㣬��A����BMP��60�㣬ֱ��д��BP�ij���
��ͼ����Rt��ACB�У���C=90�㣬AC=16cm��BC=8cm������P�ӵ�C��������CA�����˶�������Qͬʱ�ӵ�B��������BC�����˶��������P���˶��ٶ�Ϊ4cm/s��Q����˶��ٶ�Ϊ2cm/s����ô�˶�����ʱ����ABC�͡�PCQ���ƣ�
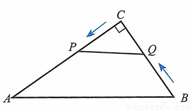
������ʮһ��У�Ļ��������У����꼶ʮ����1��������2��Ů�����������������2��������2��Ů��������ֽ���
��1���ӻ�������������ֽ���7��ѧ����ѡȡ1���μӰ佱��ᣬ��պ��������ĸ��ʣ�
��2���ֱ�ӻ�������������ֽ���ѧ���и�ѡȡ1���μӰ佱��ᣬ���б�����״ͼ��պ���һ����һŮ���ĸ��ʣ�
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
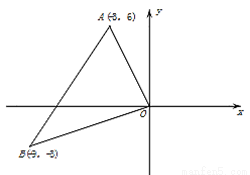
��ͼ����ƽ��ֱ������ϵ�У���֪��A��-3��6����B��-9��-3������ԭ��OΪλ�����ģ����Ʊ�Ϊ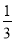 ���ѡ�ABO��С�����A�Ķ�Ӧ��A���������( )
���ѡ�ABO��С�����A�Ķ�Ӧ��A���������( )
A. ��-1��2�� B. ��-1��2����1��-2��
C. ��-9��18����9��-18�� D. ��1��-2��
B ������������������ߵ�A��-3��6������ԭ��OΪλ�����ģ����Ʊ�Ϊ���ѡ�ABO��С�� ���A�Ķ�Ӧ��A��������ǣ�-1��2����1��-2���� ��ѡB�� �㾦����ƽ��ֱ������ϵ�У����λ�Ʊ任����ԭ��Ϊλ�����ģ����Ʊ�Ϊk����ôλ��ͼ�ζ�Ӧ�������ıȵ���k��-k.��ABC���DEF�����Ʊ�Ϊ1��4�����ABC���DEF���ܳ���Ϊ���� ����
A. 1��2 B. 1��3 C. 1��4 D. 1��16
�鿴������x�ķ���x2+kx��1=0�ĸ�������ǣ�����
A. ����������ȵ�ʵ���� B. ��������ȵ�ʵ����
C. ֻ��һ��ʵ���� D. û��ʵ����
�鿴����ͼ��AD��BE��CF��ֱ��l1��l2������ƽ���߷ֱ��ڵ�A��B��C�͵�D��E��F����֪AB=1��BC=3��DE=2����DF�ij�Ϊ�� ��
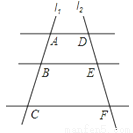
A. 4 B. 5 C. 6 D. 8
�鿴����ɽ����2015��ˮ������Ϊ100�֣�2017��ˮ������Ϊ144�֣���ù�ˮ����������ƽ��������.��ù�ˮ����������ƽ��������Ϊ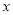 �������������з���Ϊ�� ��
�������������з���Ϊ�� ��
A. 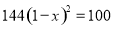 B.
B. 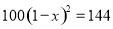
C. 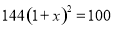 D.
D. 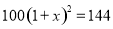
Ҫ��Сǿ��С����С�����������ѡ������Ϊ���֣���Сǿ��С��ͬʱ��ѡ�ĸ�����( )
A. 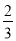 B.
B. 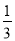 C.
C. 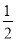 D.
D. 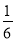
- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
����2x2��5x+3��3x2+6x��1��
�� ��������������������ҳ���Ŀ�е�ͬ����ٸ��ݺϲ�ͬ����ķ���ϵ�������Ϊϵ������ĸ����ĸ��ָ�����䣮 ����������������� ԭʽ=����2��3��x2+����5+6��x+��3��1��=��5x2+x+2�� �㾦��������Ҫ����ϲ�ͬ����ķ��ؼ�������ϵ�������Ϊϵ������ĸ����ĸ��ָ�����䣮�ϲ�ͬ�����м�©������Ǵ�����ķ��ţ�����ͬ�����ϵ����Ϊ�෴������ϲ�����Ϊ0�� ...��a=��1��b=1ʱ�������д���ʽ��ֵ��
��1����3a+2b����2a��b����
��2��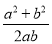 ��
��
���㣺
��1��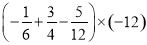 ��
��
��2��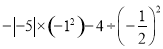 ��
��
���㣺2xy2��3xy2=__��
�鿴����ʽ��2x+y��ֵ�ǩ�4����4x+2y+8��ֵ��_____��
�鿴�����㣺 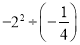 =_____��
=_____��
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������


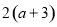 ��ֵ��
��ֵ��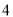 ��Ϊ�෴������
��Ϊ�෴������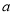 ��ֵΪ______��
��ֵΪ______��