题目内容
3.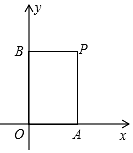 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴、y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴、y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.(1)判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,3)在直线y=-x+b(b为常数)上,求a,b的值;
(3)若直线y=2x+12上存在和谐点,写出此点的坐标:(($\frac{-3+\sqrt{57}}{2}$,9$+\sqrt{57}$)或($\frac{-3-\sqrt{57}}{2}$,9-$\sqrt{57}$)).
分析 (1)根据题意即可得到结论;
(2)因为P(a,3)是和谐点,所以根据题意得3×|a|=2×(|a|+3).①当a>0时,②当a<0时,列方程即可得到结论;
(3)设此点的坐标为(a,2a+12),由题意列方程即可得到结论.
解答 解:(1)M不是和谐点,N是和谐点.
根据题意,对于M而言,面积为1×2=2,周长为2×(1+2)=6,
所以M不是和谐点,
对于N而言,面积为4×4=16,周长为2×(4+4)=16,
所以N是和谐点.
(2)因为P(a,3)是和谐点,
所以根据题意得3×|a|=2×(|a|+3).
①当a>0时,3a=2(a+3),3a=2a+6,
解得a=6,将(6,3)代入y=-x+b得3=-6+b,
解得b=9.
②当a<0时,-3a=2(-a+3),-3a=-2a+6,
解得a=-6,将(-6,3)代入y=-x+b得3=6+b,
解得b=-3.
所以a=6,b=9或a=-6,b=-3.
(3)设此点的坐标为(a,2a+12),
由题意得,a(2a+12)=2(a+2a+12),
∴a=$\frac{-3±\sqrt{57}}{2}$,
∴P($\frac{-3+\sqrt{57}}{2}$,9$+\sqrt{57}$)或($\frac{-3-\sqrt{57}}{2}$,9-$\sqrt{57}$).
故答案为:($\frac{-3+\sqrt{57}}{2}$,9$+\sqrt{57}$)或($\frac{-3-\sqrt{57}}{2}$,9-$\sqrt{57}$).
点评 题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b);直线上任意一点的坐标都满足函数关系式y=kx+b.

| A. | a | B. | a2 | C. | a4 | D. | a5 |

按照上面的规律,摆n个“金鱼”需要用火柴的根数为( )
| A. | 2+6n | B. | 8+6n | C. | 4+4n | D. | 8n |
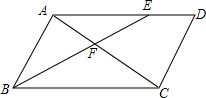 如图,在?ABCD中,点E在AD边上,BE交对角线AC于点F,则下列各式错误的是( )
如图,在?ABCD中,点E在AD边上,BE交对角线AC于点F,则下列各式错误的是( )| A. | $\frac{AF}{CF}=\frac{EF}{BF}$ | B. | $\frac{AF}{BF}=\frac{EF}{CF}$ | C. | $\frac{BF}{BE}=\frac{CF}{AC}$ | D. | $\frac{AF}{EF}=\frac{CF}{BF}$ |
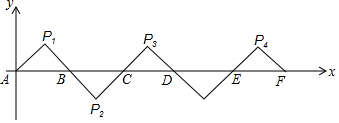
| A. | (4033,-1) | B. | (4031,-1) | C. | (4033,1) | D. | (4031,1) |
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 直角三角形 | D. | 钝角三角形或直角三角形 |
 的结果是( )
的结果是( )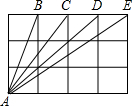 如图,在边长为1的正方形网格中,有四条线段AB,AC,AE和AD,点A,B,C,D,E都是小正方形的顶点,在上面四条线段中,长度是无理数的线段有( )
如图,在边长为1的正方形网格中,有四条线段AB,AC,AE和AD,点A,B,C,D,E都是小正方形的顶点,在上面四条线段中,长度是无理数的线段有( )


