题目内容
11.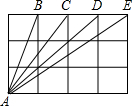 如图,在边长为1的正方形网格中,有四条线段AB,AC,AE和AD,点A,B,C,D,E都是小正方形的顶点,在上面四条线段中,长度是无理数的线段有( )
如图,在边长为1的正方形网格中,有四条线段AB,AC,AE和AD,点A,B,C,D,E都是小正方形的顶点,在上面四条线段中,长度是无理数的线段有( )| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |
分析 先根据勾股定理求出AB,AC,AD,AE这4条线段的长度,然后判断哪些是无理数.
解答  解:根据勾股定理计算得:
解:根据勾股定理计算得:
在直角△ABM中,AB=$\sqrt{B{M}^{2}+A{M}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
同理可得:AC=$\sqrt{13}$;AD=3$\sqrt{2}$;AE=5;
所以长度是无理数的线段有AB,AC,AD.
故选B.
点评 此题主要考查学生对勾股定理及无理数的理解及运用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
4.下列各数:$\frac{π}{2}$,0,$\sqrt{9}$,0.$\stackrel{•}{2}$$\stackrel{•}{3}$,$\frac{22}{7}$,0.303003…,1-$\sqrt{2}$中无理数个数为( )
| A. | 2 个 | B. | 3 个 | C. | 4 个 | D. | 5 个 |
19.下列各组线段中,成比例线段的组是( )
| A. | 3cm,4cm,5cm,8cm | B. | 1cm,3cm,4cm,8cm | C. | 2cm,3cm,4cm,6cm | D. | 2cm,6cm,4cm,8cm |
6.在-2,$\sqrt{9}$,$\sqrt{2}$,0,-π中,有理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.下列四个数中,最小的数是( )
| A. | -$\frac{1}{3}$ | B. | -3 | C. | 0 | D. | $\frac{1}{3}$ |
20.下列各式中,计算错误的是( )
| A. | 2a+3a=5a | B. | 2x-3x=-1 | C. | -x(2-x)=x2-2x | D. | (-x3)2=x6 |
1.下列各组式子中,是同类项的是( )
| A. | $\frac{1}{5}$mn与5m2n | B. | 5ab与5abc | C. | 2x2y与2a2b | D. | 2x3y2与$\frac{1}{2}$y2x3 |
 如图,△ABC是等边三角形,边长为5,D为AC边上一动点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于E,连接DE,则△BDE的面积的最小值为$\frac{75\sqrt{3}}{8}$.
如图,△ABC是等边三角形,边长为5,D为AC边上一动点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于E,连接DE,则△BDE的面积的最小值为$\frac{75\sqrt{3}}{8}$.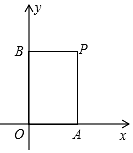 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴、y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴、y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.