某学校在一次数学活动课中.举行用火柴摆“摆金鱼活动.如图所示:按照上面的规律.摆n个“金鱼需要用火柴的根数为( )A．2+6nB．8+6nC．4+4nD．8n 题目和参考答案——青夏教育精英家教网—

题目内容

18．某学校在一次数学活动课中，举行用火柴摆“摆金鱼”活动，如图所示：

按照上面的规律，摆n个“金鱼”需要用火柴的根数为（　　）

A．

2+6n

B．

8+6n

C．

4+4n

D．

分析观察给出的3个例图，注意火柴棒根数的变化是图②的火柴棒比图①的多6根，图③的火柴棒比图②的多6根，而图n的火柴棒的根数为2n+6．

解答解：由图形可知：
第一个金鱼需用火柴棒的根数为：2+6=8；
第二个金鱼需用火柴棒的根数为：2+2×6=14；
第三个金鱼需用火柴棒的根数为：2+3×6=20；
…；
第n个金鱼需用火柴棒的根数为：2+n×6=2+6n．
故选：A．

点评本题考查列代数式，本题的解答体现了由特殊到一般的数学方法（归纳法），先观察特例，找到火柴棒根数的变化规律，然后猜想第n条小鱼所需要的火柴棒的根数．

练习册系列答案

	A．	三条直线两两相交有三个交点
	B．	过一点有且只有一条直线与已知直线垂直
	C．	同旁内角互补
	D．	直线外一点与直线上所有点的连线段中，垂线段最短

6．在-2，$\sqrt{9}$，$\sqrt{2}$，0，-π中，有理数的个数是（　　）

13．12×$\frac{5}{6}$的结果是（　　）

3．

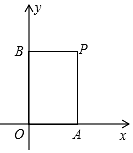在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成矩形的周长与面积相等，则这个点叫做和谐点．例如，图中过点P分别作x轴、y轴的垂线，与坐标轴围成矩形OAPB的周长与面积相等，则点P是和谐点．
（1）判断点M（1，2），N（4，4）是否为和谐点，并说明理由；
（2）若和谐点P（a，3）在直线y=-x+b（b为常数）上，求a，b的值；
（3）若直线y=2x+12上存在和谐点，写出此点的坐标：（（$\frac{-3+\sqrt{57}}{2}$，9$+\sqrt{57}$）或（$\frac{-3-\sqrt{57}}{2}$，9-$\sqrt{57}$））．

10．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）

2^-1

8．四舍五入得到的近似数0.983，它的精确度是精确到（　　）

试题分类