题目内容
13.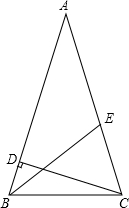 如图,在△ABC中,AB=AC,CD⊥AB,CE=2BD.
如图,在△ABC中,AB=AC,CD⊥AB,CE=2BD.(1)求证:BE=BC.
(2)在(1)的条件下,BE=AE,求∠DCB的度数.
分析 (1)作BF⊥AC于点F,易证BF是CE的中垂线,则BE=BC;
(2)设∠A=x°,则根据等边对等角即可利用x表示出∠ABC和∠ACB的度数,然后在△ABC中利用三角形内角和定理即可求得x的度数,然后在直角△BCD中利用内角和定理求解.
解答 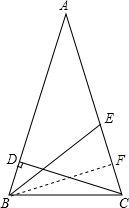 (1)证明:作BF⊥AC于点F.
(1)证明:作BF⊥AC于点F.
∵S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BF,AB=AC,
∴CD=BF.
∴BD=CF,
又∵CE=2BD,
∴EF=FC,
又∵BF⊥AC,
∴BC=BE;
(2)设∠A=x°,
∵BE=AE,
∴∠ABE=∠A=x°,
∴∠BEC=∠A+∠ABE=2x°,
∵BE=BC,
∴∠ACB=∠BEC=2x°,
又∵AB=AC,
∴∠ABC=∠ACB=2x°,
∵△ABC中∠A+∠ABC+∠ACB=180°,即x+2x+2x=180,
解得:x=36,
则∠ABC=72°,
∴直角△BCD中,∠BCD=90°-72°=18°.
点评 本题考查了等腰三角形的性质以及三角形的内角和定理,正确作出辅助线是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.小月从每月的零花钱中省出x元钱捐给希望工程,一年下来小月共捐款( )
| A. | 10x | B. | 12x元 | C. | 12元 | D. | (12+x) 元 |
5.一元二次方程x2+1=2x的根的情况是( )
| A. | 没有实数根 | B. | 有两个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
3.下列说法中正确的是( )
| A. | 单项式-$\frac{2}{3}$a2b的系数为-2 | B. | 多项式-3a2b+7a2b2+1的次数是3 | ||
| C. | a和0都是单项式 | D. | x2+$\frac{2}{y}$是整式 |
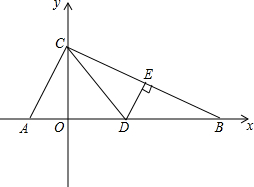 如图,在平面直角坐标系内,已知A(-4,0),B(16,0),点C在y轴正半轴上,且∠ACB=90°,D,E分别为线段AB,BC上的点,把△BDE沿直线DE翻折,使点B落在点C处.
如图,在平面直角坐标系内,已知A(-4,0),B(16,0),点C在y轴正半轴上,且∠ACB=90°,D,E分别为线段AB,BC上的点,把△BDE沿直线DE翻折,使点B落在点C处.