题目内容
8.解下列方程(1)$\frac{2-x}{x-3}$+$\frac{1}{3-x}$=1
(2)2x2-10x=3.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)方程整理后,利用公式法求出解即可.
解答 解:(1)去分母得:2-x-1=x-3,
移项合并得:2x=4,
解得:x=2,
经检验x=2是分式方程的解;
(2)方程整理得:2x2-10x-3=0,
这里a=2,b=-10,c=-3,
∵△=100+24=124,
∴x=$\frac{10±2\sqrt{31}}{4}$=$\frac{5±\sqrt{31}}{2}$,
解得:x1=$\frac{5+\sqrt{31}}{2}$,x2=$\frac{5-\sqrt{31}}{2}$.
点评 此题考查了解分式方程,以及解一元二次方程-公式法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
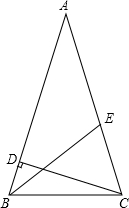 如图,在△ABC中,AB=AC,CD⊥AB,CE=2BD.
如图,在△ABC中,AB=AC,CD⊥AB,CE=2BD.