题目内容
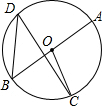
如图，△ABC内接于⊙O，AE是⊙O的直径，AE与BC交于点D，且D是OE的中点，则tan∠ABC•tan∠ACB=______．
连接BE、CE，则∠ABE=∠ACE=90°．
∵∠EAC=∠CBE，∠BED=∠ACB，
∴△ADC∽△BDE，
∴
=
．①
同理可由△ADB∽△CDE，得
=
． ②
①×②，得
=
=3．
Rt△AEC中，tan∠AEC=
．
同理得tan∠AEB=
．
故tan∠AEC•tan∠AEB=
=3．
∵∠EAC=∠CBE，∠BED=∠ACB，
∴tan∠ABC•tan∠ACB=3．
∵∠EAC=∠CBE，∠BED=∠ACB，
∴△ADC∽△BDE，
∴
| AC |
| BE |
| AD |
| BD |
同理可由△ADB∽△CDE，得
| AB |
| EC |
| BD |
| DE |
①×②，得
| AB•AC |
| BE•EC |
| AD |
| DE |
Rt△AEC中，tan∠AEC=
| AC |
| EC |
同理得tan∠AEB=
| AB |
| BE |
故tan∠AEC•tan∠AEB=
| AB•AC |
| BE•EC |
∵∠EAC=∠CBE，∠BED=∠ACB，
∴tan∠ABC•tan∠ACB=3．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
