题目内容
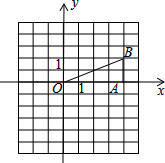 如图,在平面直角坐标系中,已知点P,M轴于A.
如图,在平面直角坐标系中,已知点P,M轴于A.(1)求tan∠BOA的值.
(2)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标.
(3)求经过B,C两点直线的函数解析式.
考点:待定系数法求一次函数解析式,坐标与图形变化-旋转,锐角三角函数的定义
专题:计算题
分析:(1)根据正切的定义求解;
(2)把Rt△OAB绕原点逆时针方向旋转90°,点B的对应点C的坐标为(-2,4);
(3)利用待定系数法求函数解析式.
(2)把Rt△OAB绕原点逆时针方向旋转90°,点B的对应点C的坐标为(-2,4);
(3)利用待定系数法求函数解析式.
解答:解 :(1)在Rt△AOB中,
:(1)在Rt△AOB中,
tan∠BOA=
=
=
;
(2)点C的坐标是(-2,4);
(3)设经过B,C两点直线的函数解析式为y=kx+b,
把点B(4,2),点C(-2,4)代入得
解得
,
所以所求的函数解析式为y=-
x+
.
 :(1)在Rt△AOB中,
:(1)在Rt△AOB中,tan∠BOA=
| AB |
| OA |
| 2 |
| 4 |
| 1 |
| 2 |
(2)点C的坐标是(-2,4);
(3)设经过B,C两点直线的函数解析式为y=kx+b,
把点B(4,2),点C(-2,4)代入得
|
|
所以所求的函数解析式为y=-
| 1 |
| 3 |
| 10 |
| 3 |
点评:本题考查了待定系数法求一次函数解析式:(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.也考查了旋转和锐角三角函数的定义.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
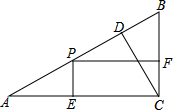 如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.
如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.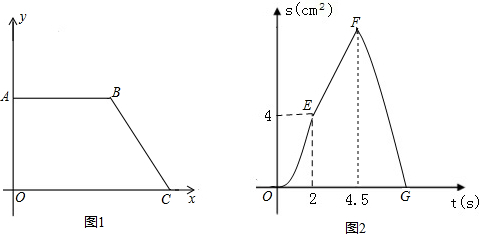
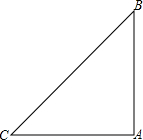 问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.当∠BAC=90°时:
问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.当∠BAC=90°时: 如图,已知正方形ABCD的边长是2,点E在DC上,△ADE经顺时针旋转后与△ABF重合.
如图,已知正方形ABCD的边长是2,点E在DC上,△ADE经顺时针旋转后与△ABF重合.