题目内容
19.若$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{mx-ny=1}\\{nx+my=8}\end{array}\right.$的解,则m、n的值是$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$.分析 先把$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$代入方程,可得$\left\{\begin{array}{l}{2m-n=1}\\{2n+m=8}\end{array}\right.$,解可求m、n的值,最后把m、n的值代入所求代数式计算即可.
解答 解:先把$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$代入方程,可得$\left\{\begin{array}{l}{2m-n=1}\\{2n+m=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$.
点评 本题考查了二元一次方程的解,解题的关键是掌握加减消元的思想.

练习册系列答案
相关题目
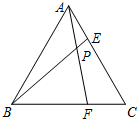 等边三角形ABC的边长为2$\sqrt{3}$,在AC,BC边上各有一个动点E,F,满足AE=CF,连接AF,BE相交于点P.
等边三角形ABC的边长为2$\sqrt{3}$,在AC,BC边上各有一个动点E,F,满足AE=CF,连接AF,BE相交于点P.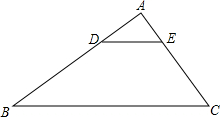 如图,在△ABC中,D为AB上一点且DE∥BC,交AC于点E,AD:AB=1:3,AC=6,BC=12.求:
如图,在△ABC中,D为AB上一点且DE∥BC,交AC于点E,AD:AB=1:3,AC=6,BC=12.求: