题目内容
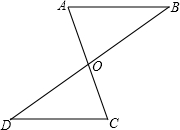
已知∠AOB与∠BOC互为邻补角,且∠BOC>∠AOB.OD平分∠AOB,射线OE使∠BOE= ∠EOC,当∠DOE=72°时,则∠EOC的度数为
∠EOC,当∠DOE=72°时,则∠EOC的度数为
- A.72°
- B.108°
- C.72°或108°
- D.以上都不对
A
分析:先根据题意画出图形,设∠AOD=∠DOB=x度,∠BOE=y度,则∠EOC=2x度,根据题意,x+y=72,再根据补角的定义即可得出y的值,故可得出结论.
解答: 解:如图1:设∠AOD=∠DOB=x度,∠BOE=y度,则∠EOC=2x度.
解:如图1:设∠AOD=∠DOB=x度,∠BOE=y度,则∠EOC=2x度.
根据题意,x+y=72,
∵2x+3y=2x+2y+y=2(x+y)+y=180,
∴2×72+y=180,
∴y=180-144=36,
∴∠EOC=36°×2=72°.
故选A.
点评:本题考查的是对顶角、邻补角,熟知对顶角、邻补角的性质是解答此题的关键.
分析:先根据题意画出图形,设∠AOD=∠DOB=x度,∠BOE=y度,则∠EOC=2x度,根据题意,x+y=72,再根据补角的定义即可得出y的值,故可得出结论.
解答:
 解:如图1:设∠AOD=∠DOB=x度,∠BOE=y度,则∠EOC=2x度.
解:如图1:设∠AOD=∠DOB=x度,∠BOE=y度,则∠EOC=2x度.根据题意,x+y=72,
∵2x+3y=2x+2y+y=2(x+y)+y=180,
∴2×72+y=180,
∴y=180-144=36,
∴∠EOC=36°×2=72°.
故选A.
点评:本题考查的是对顶角、邻补角,熟知对顶角、邻补角的性质是解答此题的关键.

练习册系列答案
相关题目
 .
.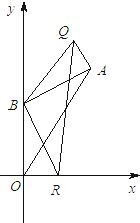 0,4),点A在第一象限.点R是x轴上的一个动点,连接BR,并把△BOR绕着点B按逆时针方向旋转,使边BO与BA重合,得到△BAQ.
0,4),点A在第一象限.点R是x轴上的一个动点,连接BR,并把△BOR绕着点B按逆时针方向旋转,使边BO与BA重合,得到△BAQ.
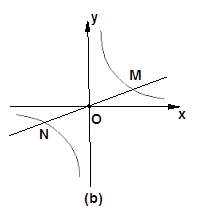
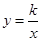 的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S
的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S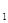 与S
与S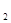 ,
,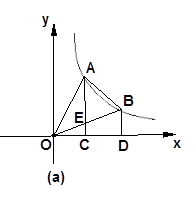
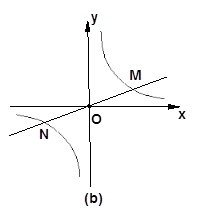
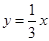 与双曲线
与双曲线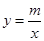 交于M、N点,且点M的纵坐标为2.
交于M、N点,且点M的纵坐标为2.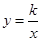 的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S
的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S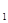 与S
与S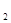 ,
,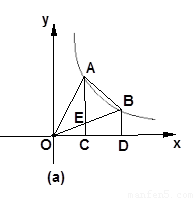
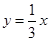 与双曲线
与双曲线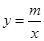 交于M、N点,且点M的纵坐标为2.
交于M、N点,且点M的纵坐标为2.