题目内容
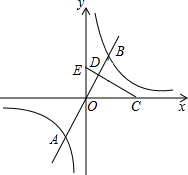
如图(a)过反比例函数![]() 的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S
的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S![]() 与S
与S![]() ,
,

1.试比较S![]() 与S
与S![]() 的大小;
的大小;
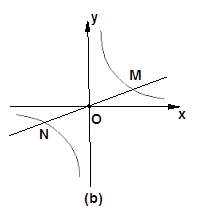
2.如图(b),已知直线![]() 与双曲线
与双曲线![]() 交于M、N点,且点M的纵坐标为2.
交于M、N点,且点M的纵坐标为2.
①求m的值;
②若过原点的另一条直线l交双曲线于P、Q两点(P点在第一象限),若由M、N、P、Q为顶点组成的四边形面积为64,求P点的坐标。
1.设![]() ,则
,则![]()
![]() , 同理
, 同理![]()
∴![]() 2分
2分
![]()
即![]() 3分
3分
∴![]()
故![]()
即![]() 4分
4分
2.①设![]() ,代入
,代入![]() ,得
,得![]() ∴
∴![]()
∴![]() 5分
5分
②由双曲线的对称性知OM=ON OP=OQ
∴四边形MPNQ是平行四边形 6分
过P, M作PH⊥![]() 轴于H MF⊥
轴于H MF⊥![]() 轴于F
轴于F
设![]() ,则
,则 ![]() ,MF=2
,MF=2
由(1)知![]()
∵S□MPNQ=64 ∴S△POM=16 7
∴![]()
即![]()
∴![]()
整理:![]() 或-18
或-18
或![]()
整理:![]() 或
或![]() 11分
11分
∵P在第一象限 ∴![]()
∴![]() 或
或![]() 12
12
解析:略

练习册系列答案
相关题目
 如图,已知正比例函数y=ax(a≠0)的图象与反比例函致
如图,已知正比例函数y=ax(a≠0)的图象与反比例函致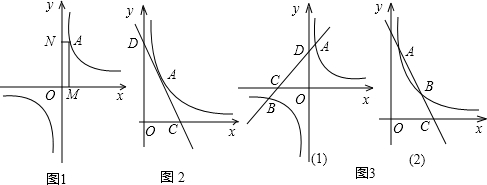
 (k为非零常数)的图象上的一动点.
(k为非零常数)的图象上的一动点.
 (k为非零常数)的图象上的一动点.
(k为非零常数)的图象上的一动点.
 点A在y轴的正半轴上,过点A作直线
点A在y轴的正半轴上,过点A作直线 ,AC:AB=2:3,则k1=( ),k2=( )。
,AC:AB=2:3,则k1=( ),k2=( )。