题目内容
 如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则DH=( )
如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则DH=( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:菱形的性质
专题:
分析:根据菱形的面积等于对角线积的一半,可求得菱形的面积,又由菱形的对角线互相平分且垂直,可根据勾股定理得AB的长,根据菱形的面积的求解方法:底乘以高或对角线积的一半,即可得菱形的高.
解答:解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=
AC=4cm,OB=OD=3cm,
∴AB=5cm,
∴S菱形ABCD=
AC•BD=AB•DH,
∴DH=
=
cm.
故选:B.
∴AC⊥BD,OA=OC=
| 1 |
| 2 |
∴AB=5cm,
∴S菱形ABCD=
| 1 |
| 2 |
∴DH=
| AC•BD |
| 2AB |
| 24 |
| 5 |
故选:B.
点评:此题考查了菱形的性质:菱形的对角线互相平分且垂直;菱形的面积的求解方法:底乘以高或对角线积的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列有关作图的叙述中,正确的是( )
| A、延长直线AB |
| B、延长射线OM |
| C、延长线段AB到C,使BC=AB |
| D、画直线AB=3cm |
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答:求相遇之后y与x之间的函数关系式,并写出自变量x的取值范围( )
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答:求相遇之后y与x之间的函数关系式,并写出自变量x的取值范围( )| A、y=240x-960,4≤x≤12 | |||||
| B、y=240x-960,4≤x≤6 | |||||
| C、y=80x,6≤x≤12 | |||||
D、y=
|
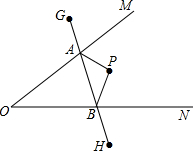 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )| A、5cm | B、10cm |
| C、20cm | D、15cm |
下列算式正确的是( )
| A、(-14)-5=-9 |
| B、0-(-3)=3 |
| C、(-3)-(-3)=-6 |
| D、|5-3|=-(5-3) |
 如图,在△ABC中,DE∥BC,AD:DB=5:3,则下列结论不正确的是( )
如图,在△ABC中,DE∥BC,AD:DB=5:3,则下列结论不正确的是( )| A、AD:AB=5:8 |
| B、AE:EC=5:3 |
| C、DE:BC=3:5 |
| D、BC:DE=8:5 |
 如图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,DE⊥BC于E,△DEC的周长是4+2
如图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,DE⊥BC于E,△DEC的周长是4+2| 2 |
A、2+
| ||
B、4+2
| ||
C、2+2
| ||
D、6+4
|
已知y=-
,下列结论中,错误的是( )
| 2 |
| x |
| A、图象必经过(-1,2) |
| B、y随x的增大而增大 |
| C、图象位于第二、四象限内 |
| D、若x>1,则-2<y<0 |
 如图,点E、C在线段BF上,且BE=CF,AB
如图,点E、C在线段BF上,且BE=CF,AB