题目内容
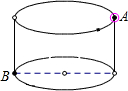 如图,有一个圆柱,它的高为15cm,底面半径为
如图,有一个圆柱,它的高为15cm,底面半径为| 8 | π |
分析:要求蚂蚁爬行的最短距离,需将圆柱的侧面展开,进而根据勾股定理得出结果.
解答: 解:如图所示:将圆柱的侧面展开为矩形,B点在矩形长的中点上,A点在矩形的宽上,则矩形长BC=
解:如图所示:将圆柱的侧面展开为矩形,B点在矩形长的中点上,A点在矩形的宽上,则矩形长BC=
×2πR=
×2π×
=8cm,AC=15cm,
在Rt△ABC中,
AB=
=
=17cm.
答:爬行的最短路程为17cm.
 解:如图所示:将圆柱的侧面展开为矩形,B点在矩形长的中点上,A点在矩形的宽上,则矩形长BC=
解:如图所示:将圆柱的侧面展开为矩形,B点在矩形长的中点上,A点在矩形的宽上,则矩形长BC=| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| π |
在Rt△ABC中,
AB=
| BC2+AC2 |
| 82+152 |
答:爬行的最短路程为17cm.
点评:本题考查的是平面展开-最短路径问题,解答此类问题的关键是在矩形上找出A和B两点的位置,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
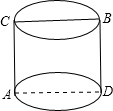 如图,有一个圆柱,它的高为9cm,底面半径为4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则沿着圆柱的表面需要爬行的最短路程是
如图,有一个圆柱,它的高为9cm,底面半径为4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则沿着圆柱的表面需要爬行的最短路程是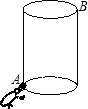 如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是
如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是 如图,有一个圆柱,它的高为13cm,底面周长为10cm,在圆柱的下底面上A点处有一个蚂蚁想吃到离上底面1cm处的B点的食物,需爬行的最短距离为
如图,有一个圆柱,它的高为13cm,底面周长为10cm,在圆柱的下底面上A点处有一个蚂蚁想吃到离上底面1cm处的B点的食物,需爬行的最短距离为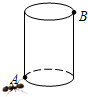 如图,有一个圆柱,它的高等于8cm,底面半径等于2
如图,有一个圆柱,它的高等于8cm,底面半径等于2