题目内容
2.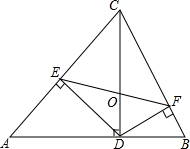 如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC.
如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC.(1)求证:CD2=CE•CA;
(2)求证:∠CEF=∠B;
(3)猜想:线段OC,OF,OE,OD成比例吗?请说明理由.
分析 (1)由一对直角相等及一对公共角相等,得到△CED与△DCA相似,根据相似三角形的性质即可得到结论;
(2)同理得到△CDF与△CBD相似,由相似得比例列出关系式,等量代换即可得证;
(3)线段OC、OD、OE、OF成比例,理由为:由∠CED=∠CFD=90°,得到C,E,D,F四点共圆,利用同弧所对的圆周角相等得到两对角相等,确定出三角形OED与三角形OCF相似,由相似得比例即可得证.
解答 解:(1)∵∠CED=∠CDA=90°,∠ECD=∠DCA,
∴△CED∽△CDA,
∴$\frac{CE}{CD}=\frac{CD}{CA}$,
即CD2=CE•CA,
(2)由(1)证得CD2=CE•CA,
同理CD2=CB•CF,
∴CA•CE=CB•CF,
∴$\frac{CE}{CB}=\frac{CF}{CA}$,
∵∠ACB=∠FCE,
∴△CEF∽△BCA,
∴∠CEF=∠B;
(3)线段OC、OD、OE、OF成比例,理由为:
∵∠CED=∠CFD=90°,
∴C,E,D,F四点共圆,
∴∠FED=∠FCD,∠DEC=∠EFC,
∴△ODE∽△OCF,
∴$\frac{OC}{OD}=\frac{OF}{OE}$,
∴线段OC、OD、OE、OF成比例.
点评 此题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
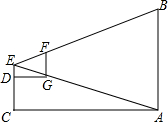 某小组选一人站在距旗杆底端A点120m的C处,把右手臂向前水平伸直,右手拿一根竖直的棍子,大拇指竖起,上下移动棍子的位置,使得一条视线经过棍子的上端点F和旗杆顶端B,另一条视线经过右手大拇指指尖G和旗杆底端A点.量得右手大拇指指尖到棍子的上端点的距离FG=23.5cm,右手臂长DG=60cm,由此,这个小组能得出旗杆AB的高吗?
某小组选一人站在距旗杆底端A点120m的C处,把右手臂向前水平伸直,右手拿一根竖直的棍子,大拇指竖起,上下移动棍子的位置,使得一条视线经过棍子的上端点F和旗杆顶端B,另一条视线经过右手大拇指指尖G和旗杆底端A点.量得右手大拇指指尖到棍子的上端点的距离FG=23.5cm,右手臂长DG=60cm,由此,这个小组能得出旗杆AB的高吗?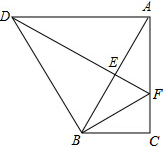 如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.
如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.