题目内容
14.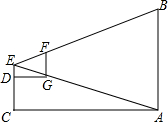 某小组选一人站在距旗杆底端A点120m的C处,把右手臂向前水平伸直,右手拿一根竖直的棍子,大拇指竖起,上下移动棍子的位置,使得一条视线经过棍子的上端点F和旗杆顶端B,另一条视线经过右手大拇指指尖G和旗杆底端A点.量得右手大拇指指尖到棍子的上端点的距离FG=23.5cm,右手臂长DG=60cm,由此,这个小组能得出旗杆AB的高吗?
某小组选一人站在距旗杆底端A点120m的C处,把右手臂向前水平伸直,右手拿一根竖直的棍子,大拇指竖起,上下移动棍子的位置,使得一条视线经过棍子的上端点F和旗杆顶端B,另一条视线经过右手大拇指指尖G和旗杆底端A点.量得右手大拇指指尖到棍子的上端点的距离FG=23.5cm,右手臂长DG=60cm,由此,这个小组能得出旗杆AB的高吗?
分析 过点E作EK⊥AB于点K,则EK=AC,EM=DG,再由FG∥AB得出△EFG∽△EBA,由相似三角形的性质即可得出结论.
解答 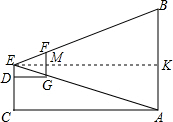 解:能.
解:能.
过点E作EK⊥AB于点K,
∵EC⊥AC,BA⊥AC,EK⊥AB,AC=120m,
∴EK=AC=120m.
同理,EM=DG=60cm=0.6m.
∵FG∥AB,FG=23.5cm=0.235m,
∴△EFG∽△EBA,
∵$\frac{FG}{AB}$=$\frac{EM}{EK}$,即$\frac{0.235}{AB}$=$\frac{0.6}{120}$,解得AB=47(m).
答:旗杆AB的高是47m.
点评 本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例,对应高的比等于相似比是解答此题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
4.下列各数中,属于负分数的是( )
| A. | -0.24 | B. | -7 | C. | $\frac{3}{4}$ | D. | 0.67 |
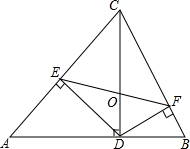 如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC.
如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC.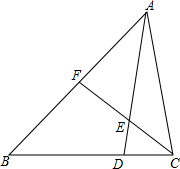 如图,F为AB中点,BD=2DC,求AE:DE的值.
如图,F为AB中点,BD=2DC,求AE:DE的值.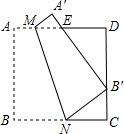 四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处.点A对应点为A′,且S△A′ME:S△CNB′=1:4,则AM的长是2.
四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处.点A对应点为A′,且S△A′ME:S△CNB′=1:4,则AM的长是2.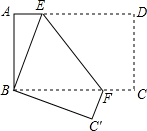 如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C′处,折痕为EF,
如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C′处,折痕为EF,