题目内容
19. 如图,点E是平行四边形ABCD中BC边的中点,连接AE和BD交于点F,若△BEF的面积为1,则四边形DCEF的面积为5.
如图,点E是平行四边形ABCD中BC边的中点,连接AE和BD交于点F,若△BEF的面积为1,则四边形DCEF的面积为5.
分析 先由平行四边形的性质得出AD=2BE,BE∥AD,进而得出△BEF∽△DAF,即可得出△ABF,△ABD,的面积,用面积的和差即可得出结论.
解答 解:∵点E是平行四边形ABCD中BC边的中点,
∴AD=BC=2BE,BE∥AD,
∴△BEF∽△DAF,
∴$\frac{EF}{AF}=\frac{BE}{AD}=\frac{1}{2}$,$\frac{{S}_{△BEF}}{{S}_{△ADF}}=(\frac{BE}{AD})^{2}=\frac{1}{4}$,
∵△BEF的面积为1,
∴S△ABF=2S△BEF=2,S△ADF=4S△BEF=4,
∴S△ABD=S△ABF+S△ADF=6,
∴S四边形DCEF=S△BCD-S△BEF=S△ABD-S△BEF=5,
故答案为:5
点评 此题是相似三角形的判定和性质,主要考查了平行四边形的性质,同高的三角形的面积比是底的比,用相似三角形的性质得出S△ABF=2S△BEF=2,S△ADF=4S△BEF=4是解本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
4.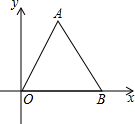 如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
 如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )
如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )| A. | (2,1) | B. | (1,2) | C. | ($\sqrt{3}$,1 ) | D. | (1,$\sqrt{3}$ ) |
9.下列各对数中,数值相等的一对是( )
| A. | -(-2)3和-23 | B. | (-3)2和-32 | C. | ($\frac{2}{3}$)2和$\frac{2^2}{3}$ | D. | |-32|和-(-32) |
 如图,学校有一块长方形草坪,少数同学会图方便走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了2m路却踩伤了花草.
如图,学校有一块长方形草坪,少数同学会图方便走“捷径”,在草坪内走出了一条“路”,他们仅仅少走了2m路却踩伤了花草.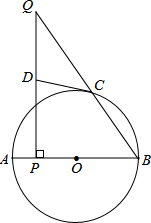 如图所示,AB为⊙O的直径,点C在⊙O上,P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q
如图所示,AB为⊙O的直径,点C在⊙O上,P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q 如图,画出△ABC关于点O中心对称的△A′B′C′.(不写画法,请保留作图痕迹)
如图,画出△ABC关于点O中心对称的△A′B′C′.(不写画法,请保留作图痕迹)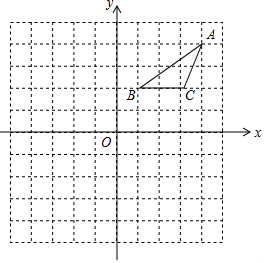 在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题;
在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4 ),请解答下列问题;