��Ŀ����
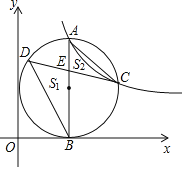
����Ŀ����֪����ͼ�����κ���y=ax2+bx��3��ͼ����x�ύ��A����1��0������B��4��0������y��Ľ���ΪC
��1������κ����Ĺ�ϵʽ��
��2����֪��M���߶�OB��һ���㣬����M��ƽ����y���ֱ��l��ֱ��l�������߽��ڵ�E����ֱ��BC���ڵ�F������CE������CEF����OBC���ƣ����M�����ꣻ
��3����֪��M��x����������һ���㣬����M��ƽ����y���ֱ��l��ֱ��l�������߽���P����ֱ��BC���ڵ�Q������CP������CPQ��CP���ۺ��Ƿ����������ֱ��l��ʹ�÷��ۺ�ĵ�Q�պ�����y���ϣ������ڣ��������ʱ��M�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��y=![]() x2��
x2��![]() x��3����2����M��������
x��3����2����M��������![]() ��0����3��0������3����M��������
��0����3��0������3����M��������![]() ��0����
��0����![]() ��0����
��0����
�������������������1�����ɴ���ϵ�������ɽ�����⣻
��2��������������ͼ1�У���CE��CFʱ����CEF�ס�OBC�����ֱ��EC�Ľ���ʽ�����÷����鼴�ɽ�����⣻����ͼ2�У���CE��EFʱ����EFC�ס�OBC����ʱE��3����3����M��3��0����
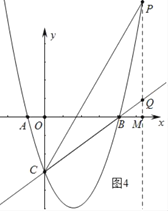
��3�����������Σ�����ͼ3�У�����Q������y��ĸ�������ʱ����P��m�� ![]() m2��
m2��![]() m��3������Q��m��
m��3������Q��m�� ![]() m��3��������ͼ4�У���ͼ3�У�����Q������y��ĸ�������ʱ����P��m��
m��3��������ͼ4�У���ͼ3�У�����Q������y��ĸ�������ʱ����P��m�� ![]() m2��
m2��![]() m��3������Q��m��
m��3������Q��m�� ![]() m��3����ͬ���ɵã�PQ��CQ���ֱ����̼��ɽ��������
m��3����ͬ���ɵã�PQ��CQ���ֱ����̼��ɽ��������
���������
�⣺��1����A����1��0������B��4��0������y��ax2��bx��3��
�õ�![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy��![]() x2��
x2��![]() x��3��
x��3��
��2������ͼ1�У���CE��CFʱ����CEF�ס�OBC��

��B��4��0����C��0����3����
��ֱ��BC�Ľ���ʽΪy��![]() x��3��
x��3��
��ֱ��CE�Ľ���ʽΪy����![]() x��3��
x��3��
�� �����
�����![]() ��
�� ��
��
����E������![]() ����
����![]() ����M��
����M��![]() ��0����
��0����
����ͼ2�У���CE��EFʱ����EFC�ס�OBC����ʱE��3����3����M��3��0��

�������������������ĵ�M������Ϊ��![]() ��0����3��0����
��0����3��0����
��3�����ڣ�����ͼ3�У�����Q������y��ĸ�������ʱ����P��m�� ![]() m2��
m2��![]() m��3������Q��m��
m��3������Q��m�� ![]() m��3����
m��3����

��PQ��CQ����
���PCQ����PCQ������CPQ��
��QC��QP����![]() m2��3m��
m2��3m��
��QM��OC��
��![]() ��
��![]() ��
��
�� ��
�� ��
��
���m��![]() ��0����������
��0����������
��M��![]() ��0����
��0����
����ͼ4�У���ͼ3�У�����Q������y��ĸ�������ʱ����P��m�� ![]() m2��
m2��![]() m��3������Q��m��
m��3������Q��m�� ![]() m��3����ͬ���ɵã�PQ��CQ��
m��3����ͬ���ɵã�PQ��CQ��
 4
4
��PQ��CQ����
���PCQ����PCQ������CPQ��
��QC��QP����![]() m2��3m��
m2��3m��
��QM��OC��
��![]() ��
��![]() ��
��
��![]() ��
�� ��
��
���m��![]() ��0����������
��0����������
��M��![]() ��0����
��0����
�������������������ĵ�M������Ϊ��![]() ��0����
��0����![]() ��0����
��0����

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�����Ŀ����ѧ�ڣ���������չ����ǡͬѧ���꣬Ʒʫ���������л���ͳʫ�ʴ����![]() С��ͳ���˰༶30��ͬѧ���·ݵ�ʫ�ʱ����������������������ʾ��
С��ͳ���˰༶30��ͬѧ���·ݵ�ʫ�ʱ����������������������ʾ��
ʫ������ | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
���� | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
��ô��30��ͬѧ���·�ʫ�ʱ�����������������λ���ֱ���![]() ����
����![]()
A. 11��7 B. 7��5 C. 8��8 D. 8��7
����Ŀ���۲��±��������Ĺ������ش��������⣺
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | ��6�� | �� | |
��1�� | -2 | 4 | -8 | a | -32 | 64 | �� |
��2�� | 0 | 6 | -6 | 18 | -30 | 66 | �� |
��3�� | -1 | 2 | -4 | 8 | -16 | b | �� |
��1����1�еĵ��ĸ���a�� ����3�еĵ�������b�� ��
��2������1�е�ijһ�е���Ϊc�����2������ͬһ�е���Ϊ ��
��3����֪��n�е��������ĺ�Ϊ2562�������1�е�n�е���Ϊx������x��ֵ��