题目内容
4. 如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.(1)求此抛物线的解析式;
(2)若点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,设点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,请说明理由.
分析 (1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.
(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.
(3)设MN交x轴于D,那么△BNC的面积可表示为:S△BNC=S△MNC+S△MNB=$\frac{1}{2}$MN(OD+DB)=$\frac{1}{2}$MN•OB,MN的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.
解答 解:(1)设抛物线的解析式为:y=a(x+1)(x-3),则:
a(0+1)(0-3)=3,a=-1;
∴抛物线的解析式:y=-(x+1)(x-3)=-x2+2x+3.
(2)设直线BC的解析式为:y=kx+b,则有:
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$;
故直线BC的解析式:y=-x+3.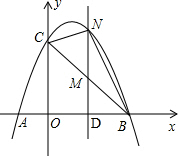 已知点M的横坐标为m,MN∥y,则M(m,-m+3)、N(m,-m2+2m+3);
已知点M的横坐标为m,MN∥y,则M(m,-m+3)、N(m,-m2+2m+3);
∴故MN=-m2+2m+3-(-m+3)=-m2+3m(0<m<3).
(3)如图;
∵S△BNC=S△MNC+S△MNB=$\frac{1}{2}$MN(OD+DB)=$\frac{1}{2}$MN•OB,
∴S△BNC=$\frac{1}{2}$(-m2+3m)•3=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$(0<m<3);
∴当m=$\frac{3}{2}$时,△BNC的面积最大,最大值为 $\frac{27}{8}$.
点评 该二次函数题较为简单,考查的知识点有:函数解析式的确定、函数图象交点坐标的求法、二次函数性质的应用以及图形面积的解法.(3)的解法较多,也可通过图形的面积差等方法来列函数关系式,可根据自己的习惯来选择熟练的解法.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案 有理数 a,b在数轴上的位置如图所示,则a+b的值( )
有理数 a,b在数轴上的位置如图所示,则a+b的值( )| A. | 大于0 | B. | 小于0 | C. | 小于 a | D. | 大于 b |

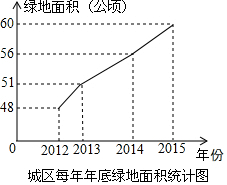 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).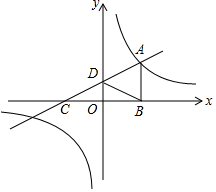 如图,直线y=$\frac{1}{2}$x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点A(m,2),与x轴交于点C,与y轴交于点D,过A作AB⊥x轴于点B,连接BD.
如图,直线y=$\frac{1}{2}$x+1与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点A(m,2),与x轴交于点C,与y轴交于点D,过A作AB⊥x轴于点B,连接BD.