题目内容
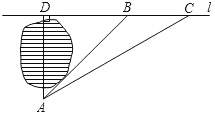
【题目】材料1:在设计人体雕塑时,存在一个分隔点,使雕塑的上部(腰以上)与下部(腰以下)之比,等于下部与全部(全身)之比,可以增加视觉美观,数学上把这个点叫“黄金分割点”. 为了研究这个点,我们在线段AB上取点C(如图1),点C把AB分成AC和CB两段,其中BC是较小的一段,现要使![]() 即可.为了简便起见,设AB=1,AC=x,则CB=1-x,代入
即可.为了简便起见,设AB=1,AC=x,则CB=1-x,代入![]() ,即
,即![]() ,也即x2+x-1=0,解之得,
,也即x2+x-1=0,解之得,![]() .所以
.所以![]() =
=![]() ,人们把
,人们把![]() 这个数叫黄金分割数,点C叫“黄金分割点”.
这个数叫黄金分割数,点C叫“黄金分割点”.
材料2:由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果![]() ,那么称直线l为该图形的“黄金分割线”.
,那么称直线l为该图形的“黄金分割线”.
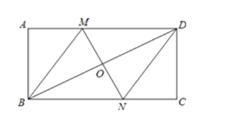
(1)如图2,点C是线段AB的黄金分割点(AC>CB),取线段AB的中点O,作点C关于点O的对称点![]() ,则
,则![]() ;继续取线段AC的中点
;继续取线段AC的中点![]() ,作点
,作点![]() 关于点
关于点![]() 的对称点
的对称点![]() ,试猜想点
,试猜想点![]() 是否线段A
是否线段A![]() 的黄金分割点,若是,请证明,若不是,请说明理由;
的黄金分割点,若是,请证明,若不是,请说明理由;
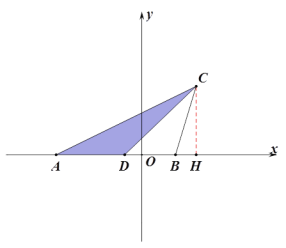
(2)如图3,在平面直角坐标系中, A(-![]() ,0),B(1,0),C(4-
,0),B(1,0),C(4-![]() ,2),求△ABC中经过点C的“黄金分割线”解析式.
,2),求△ABC中经过点C的“黄金分割线”解析式.
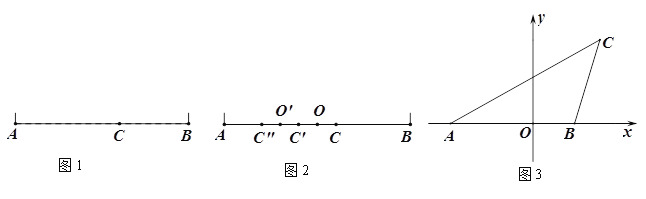
【答案】(1)![]() ,点
,点![]() 是线段A
是线段A![]() 的黄金分割点,理由详见解析;(2)
的黄金分割点,理由详见解析;(2)![]()
【解析】
(1)![]()
![]() ,根据中点及对称点的性质得到A
,根据中点及对称点的性质得到A![]() =BC,再根据线段成比例证得点
=BC,再根据线段成比例证得点![]() 是否线段A
是否线段A![]() 的黄金分割点;
的黄金分割点;
(2)过点C作CH⊥x轴于点H,分两种情况:①当![]() >
>![]() 时,②当
时,②当![]() <
<![]() 时,分别证明点D是线段AB的黄金分割点,由此求出解析式.
时,分别证明点D是线段AB的黄金分割点,由此求出解析式.
(1)![]()
点![]() 是线段A
是线段A![]() 的黄金分割点,理由如下:
的黄金分割点,理由如下:
∵OC=O![]() ,
,
∴AO - O![]() =BO-OC,
=BO-OC,
∴A![]() =BC,
=BC,
∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴点![]() 是AC的黄金分割点,
是AC的黄金分割点,
∴![]() ,
,
同理可得
![]()
∴![]()
∴![]() 是线段A
是线段A![]() 的黄金分割点
的黄金分割点
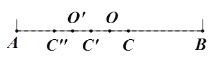
(2)设直线CD是△ABC的黄金分割线,点D的坐标为(x,0),直线CD的解析式为:![]() ,
,
过点C作CH⊥x轴于点H,
![]() ,
,![]() ,
,![]() ,
,
①当![]() >
>![]() 时,
时,
∵直线CD是△ABC的黄金分割线,
∴![]() ,
,
∴![]() ,
,
∴点D是线段AB的黄金分割点,
∴![]() =
=![]() ,
,![]() ,
,
解之得,x=2-![]() ,
,
∵直线![]() 经过D(2-
经过D(2-![]() ,0),C(4-
,0),C(4-![]() ,2),
,2),
∴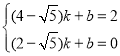 ,
,
解之得,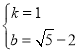 ,
,
∴![]() ;
;
②当![]() <
<![]() 时,
时,
∵直线CD是△ABC的黄金分割线,
∴![]() ,
,
∴![]() ,
,
∴点D是线段AB的黄金分割点,
∴![]() =
=![]() ,
,![]() =,
=,![]()
解之得,![]() ,
,
∵直线![]() 经过C(4-
经过C(4-![]() ,2),D(-1,0),
,2),D(-1,0),
∴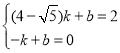 ,
,
解之得,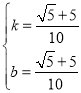 ,
,
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】一个盒子里有3个相同的小球,将3个小球分别标示号码1、2、3,每次从盒子里随机取出1个小球且取后放回,预计取球10次.若规定每次取球时,取出的号码即为得分,则前八次的取球得分情况如下表所示
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分 | 2 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
(1)设第1次至第8次取球得分的平均数为![]() ,求
,求![]() 的值:
的值:
(2)求事件“第9次和第10次取球得分的平均数等于![]() ”发生的概率;(列表法或树状图)
”发生的概率;(列表法或树状图)