题目内容
如图,直线 分别交
分别交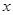 轴,
轴,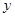 轴于
轴于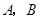 两点,以
两点,以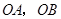 为边作矩形
为边作矩形 ,
,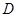 为
为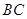 的中点.以
的中点.以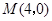 ,
,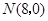 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形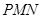 ,点
,点 在第一象限,设矩形
在第一象限,设矩形 与
与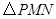 重叠部分的面积为
重叠部分的面积为 .
.
(1)求点 的坐标;
的坐标;
(2)当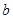 值由小到大变化时,求
值由小到大变化时,求 与
与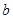 的函数关系式;
的函数关系式;
(3)若在直线 上存在点
上存在点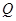 ,使
,使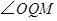 等于
等于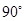 ,求出
,求出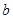 的取值范围;
的取值范围;
(4)在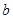 值的变化过程中,若
值的变化过程中,若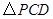 为等腰三角形,请直接写出所有符合条件的
为等腰三角形,请直接写出所有符合条件的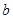 值.
值.
解: (1)作 于
于 ,则
,则 .
. ,
, .
.
(2)当 时,如图①,
时,如图①,
 .
.
当 时,如图②,
时,如图②,
设 交
交 于
于 .
. .
.
 .
.
即 .
.
或 .
.
当 时,如图③,
时,如图③,
设 交
交 于
于 .
. .
. ,
,
或 .
.
当 时,如图④,
时,如图④,
 .
.
(此问不画图不扣分)
(3) .
.
(提示:以 为直径作圆,当直线
为直径作圆,当直线

与此圆相切时, .)
.)
(4)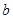 的值为
的值为 ,
, ,
, .
.
(提示:当 时,
时, .
.
当 时,
时, (舍),
(舍), .
.
当 时,
时, .)
.)
解析

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
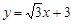 分别交
分别交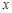 轴、
轴、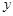 轴于B、A两点,抛物线L:
轴于B、A两点,抛物线L: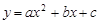 的顶点G在
的顶点G在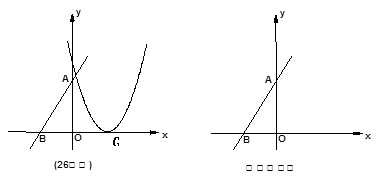
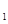 ,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L
,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L 分别交
分别交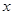 轴,
轴,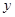 轴于点
轴于点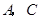 ,点
,点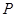 是直线
是直线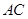 与双曲线
与双曲线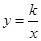 在第一象限内的交点,
在第一象限内的交点,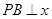 轴,垂足为点
轴,垂足为点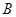 ,
,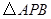 的面积为4.
的面积为4.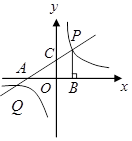
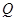 的坐标.
的坐标.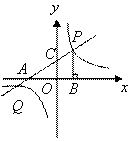
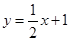 分别交
分别交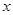 轴,
轴,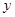 轴于点
轴于点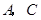 ,点
,点 是直线
是直线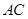 与双曲线
与双曲线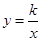 在第一象限内的交点,
在第一象限内的交点,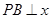 轴,垂足为点
轴,垂足为点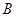 ,
,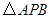 的面积为4.
的面积为4.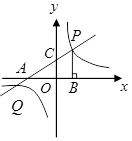
 的坐标.
的坐标.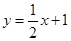 分别交
分别交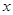 轴,
轴,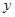 轴于点
轴于点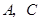 ,点
,点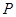 是直线
是直线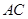 与双曲线
与双曲线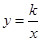 在第一象限内的交点,
在第一象限内的交点,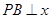 轴,垂足为点
轴,垂足为点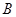 ,
,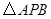 的面积为4.
的面积为4.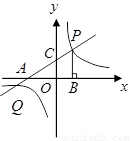
 的坐标.
的坐标.