题目内容
如图,直线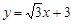 分别交
分别交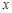 轴、
轴、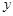 轴于B、A两点,抛物线L:
轴于B、A两点,抛物线L: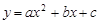 的顶点G在
的顶点G在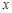 轴上,且过(0,4)和(4,4)两点.
轴上,且过(0,4)和(4,4)两点.
【小题1】求抛物线L的解析式;
【小题2】抛物线L上是否存在这样的点C,使得四边形ABGC是以BG为底边的梯形,若存在,请求出C点的坐标,若不存在,请说明理由.
【小题3】将抛物线L沿
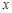 轴平行移动得抛物线L
轴平行移动得抛物线L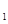 ,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L
,其顶点为P,同时将△PAB沿直线AB翻折得到△DAB,使点D落在抛物线L 上. 试问这样的抛物线L
上. 试问这样的抛物线L 是否存在,若存在,求出L
是否存在,若存在,求出L 对应的函数关系式,若不存在,说明理由.
对应的函数关系式,若不存在,说明理由.
p;【答案】
【小题1】∵抛物线L过(0,4)和(4,4)两点,由抛物线的对称性知对称轴为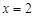 , ∴G(2,0),将(2,0)、(4,4)代入
, ∴G(2,0),将(2,0)、(4,4)代入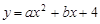 ,得
,得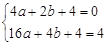 ,
,
解得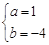 . ∴抛物线L的解析式为
. ∴抛物线L的解析式为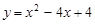 .……………………3分
.……………………3分
【小题2】∵直线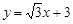 分别交
分别交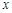 轴、
轴、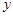 轴于B、A两点,∴A(0,3),B(-
轴于B、A两点,∴A(0,3),B(-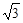 ,0).
,0).
若抛物线L上存在满足的点C,则AC∥BG,
∴C点纵坐标此为3,设C(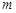 ,3),又C在抛物线L,代人解析式:
,3),又C在抛物线L,代人解析式:
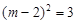 ,
, 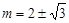 , ∴
, ∴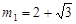 ,
,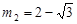 .……………………5分
.……………………5分
当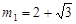 时, BG=
时, BG=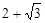 , AG=
, AG=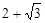 ,
,
∴BG∥AG且BG=AG,此时四边形ABGC是平行四边形,舍去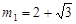 ,
,
当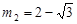 时, BG=
时, BG=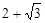 , AG=
, AG=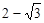 ,
,
∴BG∥AG且BG≠AG,此时四边形ABGC是梯形.
故存在这样的点C,使得四边形ABGC是以BG为底边的梯形,其坐标为:
C(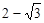 ,3). …………………………………………7分
,3). …………………………………………7分
【小题3】假设抛物线L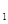 是存在的,且对应的函数关系式为
是存在的,且对应的函数关系式为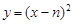 , ∴顶点P(
, ∴顶点P(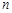 ,0).
,0).
Rt△ABO中,AO=3,BO=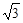 ,可得∠ABO=60°,又△ABD≌△ABP.
,可得∠ABO=60°,又△ABD≌△ABP.
∴∠ABD=60°,BD=BP=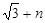 .……………………8分
.……………………8分
如图,过D作DN⊥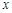 轴于N点,Rt△BND中,BD=
轴于N点,Rt△BND中,BD=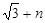 , ∠DBN=60°
, ∠DBN=60°
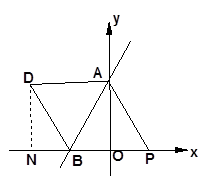
∴DN=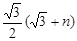 ,BN=
,BN=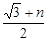 ,∴D(
,∴D(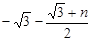 ,
,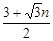 ),
),
即D(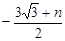 ,
,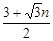 ),又D点在抛物线
),又D点在抛物线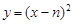 上,
上,
∴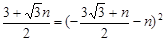 ,整理:
,整理: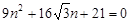 .
.
解得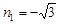 ,
,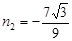 ,当
,当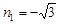 时,P与B重合,不能构成三角形,舍去,
时,P与B重合,不能构成三角形,舍去,
∴当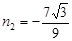 时,此时抛物线为
时,此时抛物线为 .……………………11分解析:
.……………………11分解析:
p;【解析】略
【小题1】∵抛物线L过(0,4)和(4,4)两点,由抛物线的对称性知对称轴为
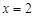 , ∴G(2,0),将(2,0)、(4,4)代入
, ∴G(2,0),将(2,0)、(4,4)代入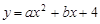 ,得
,得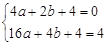 ,
,解得
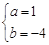 . ∴抛物线L的解析式为
. ∴抛物线L的解析式为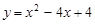 .……………………3分
.……………………3分【小题2】∵直线
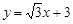 分别交
分别交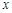 轴、
轴、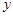 轴于B、A两点,∴A(0,3),B(-
轴于B、A两点,∴A(0,3),B(-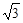 ,0).
,0). 若抛物线L上存在满足的点C,则AC∥BG,
∴C点纵坐标此为3,设C(
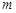 ,3),又C在抛物线L,代人解析式:
,3),又C在抛物线L,代人解析式: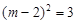 ,
, 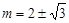 , ∴
, ∴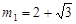 ,
,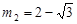 .……………………5分
.……………………5分当
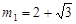 时, BG=
时, BG=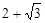 , AG=
, AG=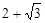 ,
, ∴BG∥AG且BG=AG,此时四边形ABGC是平行四边形,舍去
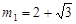 ,
,当
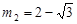 时, BG=
时, BG=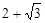 , AG=
, AG=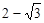 ,
,∴BG∥AG且BG≠AG,此时四边形ABGC是梯形.
故存在这样的点C,使得四边形ABGC是以BG为底边的梯形,其坐标为:
C(
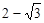 ,3). …………………………………………7分
,3). …………………………………………7分【小题3】假设抛物线L
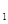 是存在的,且对应的函数关系式为
是存在的,且对应的函数关系式为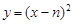 , ∴顶点P(
, ∴顶点P(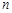 ,0).
,0).Rt△ABO中,AO=3,BO=
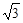 ,可得∠ABO=60°,又△ABD≌△ABP.
,可得∠ABO=60°,又△ABD≌△ABP.∴∠ABD=60°,BD=BP=
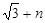 .……………………8分
.……………………8分如图,过D作DN⊥
 轴于N点,Rt△BND中,BD=
轴于N点,Rt△BND中,BD=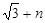 , ∠DBN=60°
, ∠DBN=60°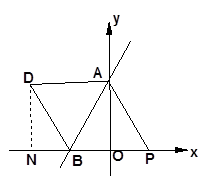
∴DN=
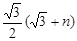 ,BN=
,BN=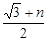 ,∴D(
,∴D(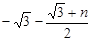 ,
,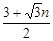 ),
), 即D(
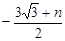 ,
,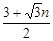 ),又D点在抛物线
),又D点在抛物线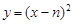 上,
上,∴
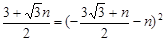 ,整理:
,整理: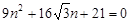 .
.解得
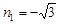 ,
,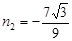 ,当
,当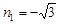 时,P与B重合,不能构成三角形,舍去,
时,P与B重合,不能构成三角形,舍去,∴当
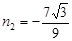 时,此时抛物线为
时,此时抛物线为 .……………………11分解析:
.……………………11分解析:p;【解析】略

练习册系列答案
相关题目
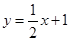 分别交
分别交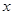 轴,
轴,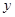 轴于点
轴于点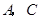 ,点
,点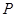 是直线
是直线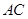 与双曲线
与双曲线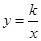 在第一象限内的交点,
在第一象限内的交点,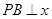 轴,垂足为点
轴,垂足为点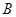 ,
,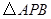 的面积为4.
的面积为4.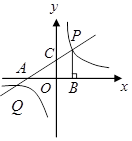
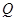 的坐标.
的坐标.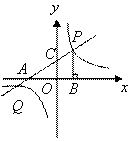
 分别交
分别交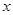 轴,
轴,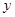 轴于点
轴于点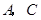 ,点
,点 是直线
是直线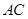 与双曲线
与双曲线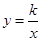 在第一象限内的交点,
在第一象限内的交点,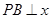 轴,垂足为点
轴,垂足为点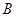 ,
,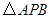 的面积为4.
的面积为4.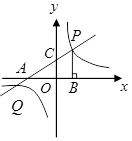
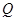 的坐标.
的坐标.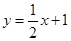 分别交
分别交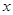 轴,
轴,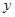 轴于点
轴于点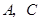 ,点
,点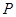 是直线
是直线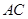 与双曲线
与双曲线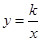 在第一象限内的交点,
在第一象限内的交点,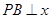 轴,垂足为点
轴,垂足为点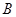 ,
,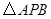 的面积为4.
的面积为4.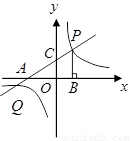
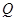 的坐标.
的坐标.