题目内容
解不等式组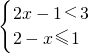
，其解集为________．
1≤x＜2
分析：先求出两个不等式的解集，再求其公共解．
解答：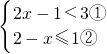
，
由①得，x＜2，
由②得，x≥1，
所以，不等式组的解集是1≤x＜2．
故答案为：1≤x＜2．
点评：本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．
分析：先求出两个不等式的解集，再求其公共解．
解答：
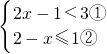，由①得，x＜2，
由②得，x≥1，
所以，不等式组的解集是1≤x＜2．
故答案为：1≤x＜2．
点评：本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．
练习册系列答案
相关题目
某童装厂现有甲种布料38米，乙种布料26米，现计划用这两种布料生产L、M两种型号的童装共50套．已知做一套L、M型号的童装所需用布料和所获得利润如下表：
（1）假设L型号的服装生产x套，请你写出满足题意的不等式组，求出其解集；并根据计算结果，设计生产方案．
（2）设用这批布料生产这两种型号的服装所获的总利润为y（元），试写出y与x之间的函数关系式，并利用函数性质说明（1）中哪种方案总利润最大？最大利润为多少？
| ′ | 甲种布料 | 乙种布料 | 获 利 |
| L型 | 0.5米 | 1米 | 45元 |
| M型 | 0.9米 | 0.2米 | 30元 |
（2）设用这批布料生产这两种型号的服装所获的总利润为y（元），试写出y与x之间的函数关系式，并利用函数性质说明（1）中哪种方案总利润最大？最大利润为多少？
