题目内容
9.平行四边形的周长为32cm,一组邻边的差为2cm,则较短边的边长为7cm.分析 如图:因为四边形ABCD是平行四边形,根据平行四边形的对边相等,可得AB=CD,AD=BC,又因为平行四边形的周长等于32cm,两邻边之差为2cm,所以可求得这个平行四边形较长的边长的长.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵平行四边形的周长等于32cm,
∴AB+CD+AD+BC=32cm,
∴AB+BC=16cm,
∵BC-AB=2cm,
∴BC=9cm,AB=7cm,
∴平行四边形的较短边的长是7cm,
故答案为7.
点评 此题考查了平行四边形的性质:平行四边形的对边相等.注意解此题需要利用方程思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.二元一次方程x-2y=4( )
| A. | 有一个解且只有一个解 | B. | 无解 | ||
| C. | 有无数多个解 | D. | 有两个解且只有两个解 |
17.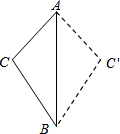 如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
 如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )
如图,将三边长分别为3、4、5的△ABC沿最长边AB翻折成△ABC′,则CC′的长为( )| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{24}{5}$ |
4.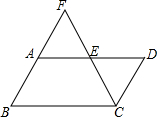 如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
 如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )
如图,在平行四边形ABCD中,点E是边AD的中点,CE与BA的延长线交于点F.若∠FCD=∠D,则下列结论不成立的是( )| A. | △AEF≌△CED | B. | CF=AD | C. | AF=CD | D. | BF=CF |
18.化简(1+$\frac{1}{a-1}$)÷$\frac{a}{{a}^{2}-2a+1}$的结果是( )
| A. | $\frac{a}{(a-1)^{2}}$ | B. | a-1 | C. | $\frac{1}{a}$ | D. | $\frac{a-1}{a}$ |
19.如图,把图①中的⊙A经过平移得到⊙O(如图②),如果图①中⊙A上一点P的坐标为(m,n),那么平移后在图②中的对应点P′的坐标为( )
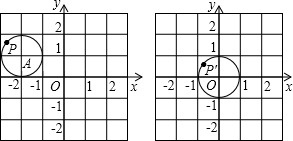

| A. | (m+2,n+1) | B. | (m-2,n-1) | C. | (m-2,n+1) | D. | (m+2,n-1) |
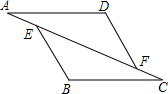 如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.
如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.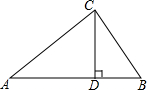 如图所示,在△ABC中,CD⊥AB于点D,若AD=2BD,AC=4,BC=3,求BD的长.
如图所示,在△ABC中,CD⊥AB于点D,若AD=2BD,AC=4,BC=3,求BD的长. 已知点A(-1,0),B(3,0),C(4,2),D(0,4).
已知点A(-1,0),B(3,0),C(4,2),D(0,4).