Question

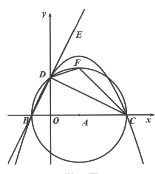
【题目】如图，已知点B的坐标是（-2，0)，点C的坐标是（8，0)，以线段BC为直径作⊙A，交y轴的正半轴于点D，过B、C、D三点作抛物线.

（1）求抛物线的解析式；

（2）连结BD，CD，点E是BD延长线上一点，∠CDE的角平分线DF交⊙A于点F，连结CF，在直线BE上找一点P，使得△PFC的周长最小，并求出此时点P的坐标；

（3）在（2）的条件下，抛物线上是否存在点G，使得∠GFC=∠DCF，若存在，请直接写出点G的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）；（3）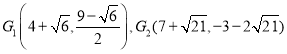

【解析】

（1）由BC是直径证得∠OCD=∠BDO,从而得到△BOD∽△DOC,根据线段成比例求出OD的长，

设抛物线解析式为y=a(x+2)(x-8),将点D坐标代入即可得到解析式；

（2）利用角平分线求出，得到，从而得出点F的坐标（3,5），再延长延长CD至点，可使,得到(-8，8)，求出F的解析式，与直线BD的交点坐标即为点P，此时△PFC的周长最小；

（3）先假设存在，①利用弧等圆周角相等把点D、F绕点A顺时针旋转90，使点F与点B重合，点G与点Q重合，则Q1(7，3),符合，求出直线FQ1的解析式，与抛物线的交点即为点G1，②根据对称性得到点Q2的坐标，再求出直线FQ2的解析式，与抛物线的交点即为点G2，由此证得存在点G.

（1）∵以线段BC为直径作⊙A,交y轴的正半轴于点D，

∴∠BDO+∠ODC=90,

∵∠OCD+∠ODC=90,

∴∠OCD=∠BDO,

∵∠DOC=∠DOB=90,

∴△BOD∽△DOC,

∴,

∵B（-2，0)，C（8，0)，

∴,

解得OD=4(负值舍去)，∴D（0,4）

设抛物线解析式为y=a(x+2)(x-8),

∴4=a(0+2)(0-8),

解得a=，

∴二次函数的解析式为y=(x+2)(x-8),即.

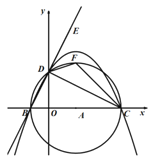
（2）∵BC为⊙A的直径，且B（-2，0)，C（8，0)，

∴OA=3,A(3,0),

∴点E是BD延长线上一点，∠CDE的角平分线DF交⊙A于点F，

∴,

连接AF，则,

∵OA=3，AF=5

∴F(3，5)

∵∠CDB=90,

∴延长CD至点，可使,

∴(-8，8)，

连接F叫BE于点P，再连接PF、PC，

此时△PFC的周长最短，

解得F的解析式为，

BD的解析式为y=2x+4,

可得交点P.

（3）存在；假设存在点G，使∠GFC=∠DCF，

设射线GF交⊙A于点Q,

①∵A(3，0),F(3，5),C(8，0),D(0，4),

∴把点D、F绕点A顺时针旋转90，使点F与点B重合，点G与点Q重合，则Q1(7，3),符合，

∵F(3，5),Q1(7，3),

∴直线FQ1的解析式为，

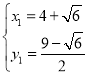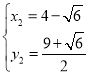解，得，（舍去），

∴G1；

②Q1关于x轴对称点Q2(7，-3),符合，

∵F(3，5),Q2(7，3),

∴直线FQ2的解析式为y=-2x+11,

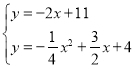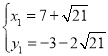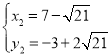解，得，（舍去），

∴G2

综上，存在点G或，使得∠GFC=∠DCF.