题目内容
【题目】现代城市绿化带在不断扩大，绿化用水的节约是一个非常重要的问题．
如图1、图2所示，某喷灌设备由一根高度为0.64 m的水管和一个旋转喷头组成，水管竖直安装在绿化带地面上，旋转喷头安装在水管顶部（水管顶部和旋转喷头口之间的长度、水管在喷灌区域上的占地面积均忽略不计），旋转喷头可以向周围喷出多种抛物线形水柱，从而在绿化带上喷灌出一块圆形区域．现测得喷的最远的水柱在距离水管的水平距离3 m处达到最高，高度为1 m．
（1）求喷灌出的圆形区域的半径；
（2）在边长为16 m的正方形绿化带上固定安装三个该设备，喷灌区域可以完全覆盖该绿化带吗？如果可以，请说明理由；如果不可以，假设水管可以上下调整高度，求水管高度为多少时，喷灌区域恰好可以完全覆盖该绿化带．（以上需要画出示意图，并有必要的计算、推理过程）
【答案】（1）8m；（2）不可以，水管高度调整到0.7m，理由见解析.
【解析】
（1）根据题意设最远的抛物线形水柱的解析式为
，然后将（0,0.64）代入解析式求得a的值，然后求解析式y=0时，x的值，从而求得半径；（2）利用圆与圆的位置关系结合正方形，作出三个等圆覆盖正方形的图形，然后利用勾股定理求得圆的半径，从而使问题得解.
解：（1）由题意，设最远的抛物线形水柱的解析式为，将（0,0.64）代入解析式，得
解得：
∴最远的抛物线形水柱的解析式为
当y=0时，
解得：
所以喷灌出的圆形区域的半径为8m；
（2）如图，三个等圆覆盖正方形
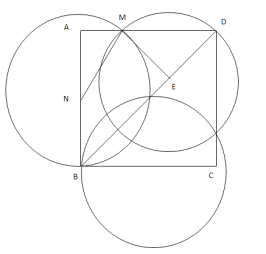
设圆的半径MN=NB=ME=DE=r，则AN=16-r,,MD=
,AM=16-
∴在Rt△AMN中，
解得：
（其中
，舍去）
∴
设最远的抛物线形水柱的解析式为，将（8.5,0）代入
解得: 
∴
当x=0时，y=
∴水管高度约为0.7m时，喷灌区域恰好可以完全覆盖该绿化带
