题目内容
解答题:
(1)计算|-3|-(
-π)0+(
)-1+(-1)3
(2)因式分解:m2(m-1)+4(1-m)
(3)化简(a+1)2-2(a+1)(a-1)+(a+2)(a-1)
(4)解方程组
(5)解不等式组
并把解集在数轴上表示出来.
(1)计算|-3|-(
| 5 |
| 1 |
| 4 |
(2)因式分解:m2(m-1)+4(1-m)
(3)化简(a+1)2-2(a+1)(a-1)+(a+2)(a-1)
(4)解方程组
|
(5)解不等式组
|
考点:实数的运算,整式的混合运算,提公因式法与公式法的综合运用,解二元一次方程组,解一元一次不等式组
专题:
分析:(1)先分别根据0指数幂及负整数指数幂的运算法则计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先提取公因式,再根据平方差公式解答即可;
(3)先把各项展开,再合并同类项即可;
(4)先用代入法求出y的值,再把y的值代入①求出x的值即可;
(5)分别求出各不等式的解集,再在数轴上表示出来即可.
(2)先提取公因式,再根据平方差公式解答即可;
(3)先把各项展开,再合并同类项即可;
(4)先用代入法求出y的值,再把y的值代入①求出x的值即可;
(5)分别求出各不等式的解集,再在数轴上表示出来即可.
解答:解:(1)原式=3-1+4-1
=5;
(2)原式=(m-1)(m2-4)
=(m-1)(m+2)(m-2);
(3)原式=a2+2a+1-2(a2-1)+a2+a-2
=3a+1;
(4)
,把①代入②得,2y+9=11,解得y=1,把y=1代入①得,x=4,
故此方程组的解为:
;
(5)
,由①得,x≤1,由②得,x>-2,
故此方程组的解为-2<x≤1,
在数轴上表示为:
 .
.
=5;
(2)原式=(m-1)(m2-4)
=(m-1)(m+2)(m-2);
(3)原式=a2+2a+1-2(a2-1)+a2+a-2
=3a+1;
(4)
|
故此方程组的解为:
|
(5)
|
故此方程组的解为-2<x≤1,
在数轴上表示为:
 .
.点评:本题考查的是实数的运算,熟知实数混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、3,4,3,5,5,2这组数据的众数是3 | ||||||||
| B、为了解参加运动会的运动员的年龄情况,从中抽了100名运动员的年龄,在这里100名运动员是抽取的一个样本 | ||||||||
C、如果数据x1,x2…xn的平均数是
| ||||||||
| D、一组表据的方差是S2,将这组数据中的每个数据都乘以3,所得的一组新数据的方差是3S2 |
一个圆锥的底面直径为6,侧面展开图为半圆,则圆锥的侧面积是( )
| A、9π | B、18π |
| C、27π | D、39π |
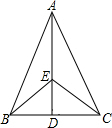 如图所示,已知AB=AC,BE=CE,求证:BD=CD.
如图所示,已知AB=AC,BE=CE,求证:BD=CD. 如图,从教室到图书馆总有少数同学不走人行道而横穿草坪,虽然明知不对,可他们还是要这样做,用我们所学的数学知识可以解释他们的动机:
如图,从教室到图书馆总有少数同学不走人行道而横穿草坪,虽然明知不对,可他们还是要这样做,用我们所学的数学知识可以解释他们的动机: