题目内容
在等腰三角形ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为( )A.7
B.7或11
C.11
D.7或10
【答案】分析:因为已知条件给出的15或12两个部分,哪一部分是腰长与腰长一半的和不明确,所以分两种情况讨论.
解答: 解:根据题意,
解:根据题意,
①当15是腰长与腰长一半时,即AC+ AC=15,解得AC=10,
AC=15,解得AC=10,
所以底边长=12- ×10=7;
×10=7;
②当12是腰长与腰长一半时,AC+ AC=12,解得AC=8,
AC=12,解得AC=8,
所以底边长=15- ×8=11.
×8=11.
所以底边长等于7或11.
故选B.
点评:本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确给出哪一部分长要一定要想到两种情况,此题要采用分类进行讨论,还应验证各种情况是否能构成三角形,这点非常重要,也是解题的关键.这也是学生容易忽视的地方,应注意向学生特别强调.
解答:
 解:根据题意,
解:根据题意,①当15是腰长与腰长一半时,即AC+
 AC=15,解得AC=10,
AC=15,解得AC=10,所以底边长=12-
 ×10=7;
×10=7;②当12是腰长与腰长一半时,AC+
 AC=12,解得AC=8,
AC=12,解得AC=8,所以底边长=15-
 ×8=11.
×8=11.所以底边长等于7或11.
故选B.
点评:本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确给出哪一部分长要一定要想到两种情况,此题要采用分类进行讨论,还应验证各种情况是否能构成三角形,这点非常重要,也是解题的关键.这也是学生容易忽视的地方,应注意向学生特别强调.

练习册系列答案
相关题目
 如图:在等腰三角形ABC中,AB=AC,∠A=40°,则∠B=
如图:在等腰三角形ABC中,AB=AC,∠A=40°,则∠B=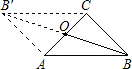 在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距
在等腰三角形ABC中,∠C=90°,BC=2cm.如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,那么点B′与点B的原来位置相距 如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积.
如图所示,在等腰三角形ABC中,AB=AC=13cm,底边BC=10cm,求底边上的高AD和△ABC的面积. 如图,在等腰三角形ABC中,两底角的平分线BE和CD相交于点0,则△OBC是
如图,在等腰三角形ABC中,两底角的平分线BE和CD相交于点0,则△OBC是