题目内容
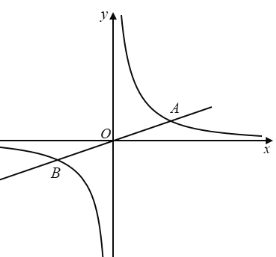
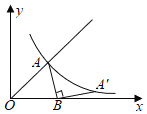
【题目】如图,函数y=x(x≥0)的图象与反比例函数y=![]() 的图象交于点A,若点A绕点B(
的图象交于点A,若点A绕点B(![]() ,0)顺时针旋转90°后,得到的点A'仍在y=
,0)顺时针旋转90°后,得到的点A'仍在y=![]() 的图象上,则点A的坐标为_____.
的图象上,则点A的坐标为_____.
【答案】(2![]() ,2
,2![]() ).
).
【解析】
设点A的坐标为(a,a),过A作AC⊥x轴于C,过A′作A′D⊥x轴于D,于是得到∠ACB=∠A′DB=90°,AC=OC=a,求得BC=![]() ,根据全等三角形的性质得到BD=AC=a,A′D=BC=
,根据全等三角形的性质得到BD=AC=a,A′D=BC=![]() ,列方程组即可得到结论.
,列方程组即可得到结论.
解:设点A的坐标为(a,a),
过A作AC⊥x轴于C,过A′作A′D⊥x轴于D,

∴∠ACB=∠A′DB=90°,AC=OC=a,
∴BC=![]() ,
,
∵点A绕点B(![]() ,0)顺时针旋转90°后,得到的点A',
,0)顺时针旋转90°后,得到的点A',
∴∠ABA′=90°,AB=A′B,
∴∠CAB+∠ABC=∠ABC+∠A′BD=90°,
∴∠CAB=∠A′BD,
∴△ACB≌△BDA′(AAS),
∴BD=AC=a,A′D=BC=![]() ,
,
∵点A'在y=![]() 的图象上,
的图象上,
∴ ,
,
解得:k=8,a=2![]() ,
,
∴点A的坐标为(2![]() ,2
,2![]() ),
),
故答案为:(2![]() ,2
,2![]() ).
).

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目