题目内容
函数y=x+1与x轴交点为
- A.（0，-1）
- B.（1，0）
- C.（0，1）
- D.（-1，0）
D
分析：由于x轴上点的坐标为（x，0），代入解析式即可求得x的值，从而得到函数与x轴的交点坐标．
解答：设函数y=x+1与x轴交点为（x，0），
将（x，0）其代入y=x+1得，
x+1=0，
解得x=-1．
所以，函数y=x+1与x轴交点为（-1，0）．
故选D．
点评：此题考查了一次函数图象上点的坐标特征，解答此题的关键是明确x轴上的点的纵坐标为0．
分析：由于x轴上点的坐标为（x，0），代入解析式即可求得x的值，从而得到函数与x轴的交点坐标．
解答：设函数y=x+1与x轴交点为（x，0），
将（x，0）其代入y=x+1得，
x+1=0，
解得x=-1．
所以，函数y=x+1与x轴交点为（-1，0）．
故选D．
点评：此题考查了一次函数图象上点的坐标特征，解答此题的关键是明确x轴上的点的纵坐标为0．
练习册系列答案
字词句段篇系列答案
相关题目
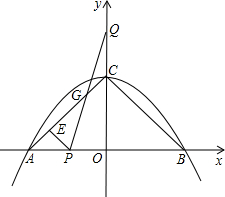正方向运动，运动时间为t秒，点P到达B点时，点Q同时停止运动．设PQ交直线AC于点G．
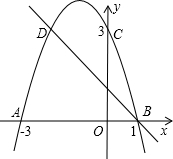0，3），点C、D是二次函数图象上的一对对称点．一次函的图象过点B、D．
二次函数的图象与x轴交于A，B两点，与y轴交于点C，如图所示，AC=2