题目内容
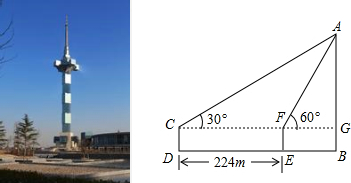
盐城电视塔是我市标志性建筑之一．如图，在一次数学课外实践活动中，老师要求测电视塔的高度AB．小明在D处用高1.5m的测角仪CD，测得电视塔顶端A的仰角为30°，然后向电视塔前进224m到达E处，又测得电视塔顶端A的仰角为60°．求电视塔的高度AB．（
取1.73，结果精确到0.1m）
| 3 |
考点：解直角三角形的应用-仰角俯角问题
专题：几何图形问题
分析：设AG=x，分别在Rt△AFG和Rt△ACG中，表示出CG和GF的长度，然后根据DE=224m，求出x的值，继而可求出电视塔的高度AB．
解答：解：设AG=x，
在Rt△AFG中，
∵tan∠AFG=
，
∴FG=
，
在Rt△ACG中，
∵tan∠ACG=
，
∴CG=
=
x，
∴
x-
=224，
解得：x≈193.8．
则AB=193.8+1.5=195.3（米）．
答：电视塔的高度AB约为195.3米．
在Rt△AFG中，
∵tan∠AFG=
| AG |
| FG |
∴FG=
| x | ||
|
在Rt△ACG中，
∵tan∠ACG=
| AG |
| CG |
∴CG=
| x |
| tan30° |
| 3 |
∴
| 3 |
| x | ||
|
解得：x≈193.8．
则AB=193.8+1.5=195.3（米）．
答：电视塔的高度AB约为195.3米．
点评：本题考查了解直角三角形的应用，关键是根据仰角构造直角三角形，利用三角函数求解，注意利用两个直角三角形的公共边求解是解答此类题型的常用方法．
练习册系列答案
相关题目
下列运算中正确的是（ ）
| A、x+2x=3x2 |
| B、x2•x3=x5 |
| C、x3÷x=3 |
| D、（-x）3=x3 |
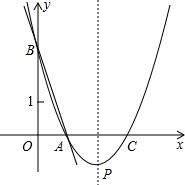如图，直线y=-3x+3与x轴、y轴分别交于点A、B，抛物线y=a（x-2）2+k经过点A、B，并与X轴交于另一点C，其顶点为P．
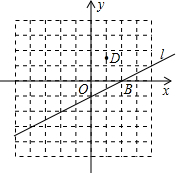如图，已知直线l的解析式为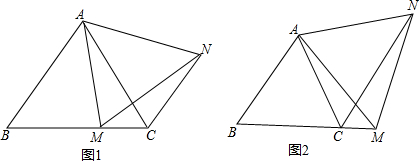y=
实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=-200x2+400x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=