题目内容
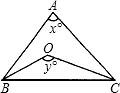 如图,若O是△ABC的内角的平分线交点,∠A=x°,∠BOC=y°,求y与x函数关系式,并指出自变量x的取值范围.
如图,若O是△ABC的内角的平分线交点,∠A=x°,∠BOC=y°,求y与x函数关系式,并指出自变量x的取值范围.
解:∵O是△ABC的内角的平分线交点,
∴∠OBC= ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,
∠ACB,
∴∠OBC+∠OCB
= ∠ABC+
∠ABC+ ∠ACB
∠ACB
= (∠ABC+∠ACB)
(∠ABC+∠ACB)
= (180°-x).
(180°-x).
∵∠BOC=180°-(∠OBC+∠OCB),
∴∠BOC=180°- (180-x),
(180-x),
∴y=90°+ (0<x<180).
(0<x<180).
分析:首先根据三角形内角和定理可以用x表示∠ABC+∠ACB,然后可以表示 (∠ABC+∠ACB),最后利用∠BOC=180°-
(∠ABC+∠ACB),最后利用∠BOC=180°- (∠ABC+∠ACB)即可求出y与x函数关系式,再根据三角形的内角和可以求出自变量x的取值范围.
(∠ABC+∠ACB)即可求出y与x函数关系式,再根据三角形的内角和可以求出自变量x的取值范围.
点评:本题主要利用了三角形内角和定理以及角平分线定义.根据题意,找到所求的等量关系是解决问题的关键.
∴∠OBC=
 ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,
∠ACB,∴∠OBC+∠OCB
=
 ∠ABC+
∠ABC+ ∠ACB
∠ACB=
 (∠ABC+∠ACB)
(∠ABC+∠ACB)=
 (180°-x).
(180°-x).∵∠BOC=180°-(∠OBC+∠OCB),
∴∠BOC=180°-
 (180-x),
(180-x),∴y=90°+
 (0<x<180).
(0<x<180).分析:首先根据三角形内角和定理可以用x表示∠ABC+∠ACB,然后可以表示
 (∠ABC+∠ACB),最后利用∠BOC=180°-
(∠ABC+∠ACB),最后利用∠BOC=180°- (∠ABC+∠ACB)即可求出y与x函数关系式,再根据三角形的内角和可以求出自变量x的取值范围.
(∠ABC+∠ACB)即可求出y与x函数关系式,再根据三角形的内角和可以求出自变量x的取值范围.点评:本题主要利用了三角形内角和定理以及角平分线定义.根据题意,找到所求的等量关系是解决问题的关键.

练习册系列答案
相关题目
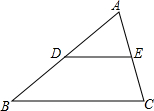 如图,若DE是△ABC的中位线,△ABC的周长为1,则△ADE的周长为( )
如图,若DE是△ABC的中位线,△ABC的周长为1,则△ADE的周长为( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
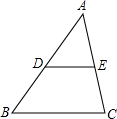 如图,若DE是△ABC的中位线,△ABC的周长为6,则△ADE的周长为( )
如图,若DE是△ABC的中位线,△ABC的周长为6,则△ADE的周长为( )| A、4 | B、3 | C、2 | D、1 |
 如图,若BD是△ABC的角平分线,则∠1=∠
如图,若BD是△ABC的角平分线,则∠1=∠ 如图,若O是△ABC内任意一点,点D,E,F分别在OA,OB,OC上,且DE∥AB,DF∥AC,AD:DO=1:2,
如图,若O是△ABC内任意一点,点D,E,F分别在OA,OB,OC上,且DE∥AB,DF∥AC,AD:DO=1:2,