题目内容

精英家教网如图，若BD是△ABC的角平分线，则∠1=∠
 
=
12
∠
 
．
分析：利用三角形一个内角的平分线的定义可知．
解答：解：∵BD是△ABC的角平分线，
∴∠1=∠2=
1
2
∠ABC．
故填∠2，∠ABC．
点评：三角形一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与所交的点间的线段叫做三角形的角平分线．
练习册系列答案
相关题目
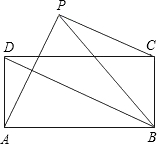精英家教网如图，若ABCD是一个长方形，AB=2，AD=1，作点A关于对角线BD的对称点P，则PC等于（　　）
A、
3
4
5
B、
1
2
5
C、
2
5
5
D、
3
5
5
（1）如图所示，BD，CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F，G，连接FG，延长AF，AG，与直线BC分别交于点M、N，那么线段FG与△ABC的周长之间存在的数量关系是什么？
即：FG=
 
（AB+BC+AC）
（直接写出结果即可）
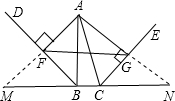
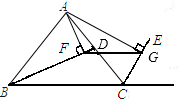
精英家教网
（2）如图，若BD，CE分别是△ABC的内角平分线；其他条件不变，线段FG与△ABC三边之间又有怎样的数量关系？请写出你的猜想，并给予证明．
精英家教网
（3）如图，若BD为△ABC的内角平分线，CE为△ABC的外角平分线，其他条件不变，线段FG与△ABC三边又有怎样的数量关系？直接写出你的猜想即可．不需要证明．答：线段FG与△ABC三边之间数量关系是
 
．
精英家教网
在△ABC中，AD是∠BAC的平分线．
（1）如图①，求证：
S△ABD
S△ACD
=
AB
AC
；
（2）如图②，若BD=CD，求证：AB=AC；
（3）如图③，若AB=5，AC=4，BC=6．求BD的长．
精英家教网
23、已知，如图，点C是AB上一点，分别以AC，BC为边，在AB的同侧作等边三角形△ACD和△BCE．
（1）指出△ACE以点C为旋转中心，顺时针方向旋转60°后得到的三角形；
（2）若AE与BD交于点O，求∠AOD的度数．

如图,直线AC‖BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA、PB,构成∠PAC、∠APB、∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是O0)

 ⑴当动点P落在第①部分时,如图1,求证:∠APB=∠PAC+∠PBD

 ⑵当动点P落在第②部分时, ∠APB=∠PAC+∠PBD是否成立?在图2中画出图形,若成立,写出推理过程,若不成立,直接写出这三个角之间的关系.

 ⑶当动点P落在第③部分时,延长BA,点P在射线BA的左侧和右侧时,分别探究∠PAC、∠APB、∠PBD之间 关系,在图3中画出图形,并直接写出相应的结论.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网