题目内容
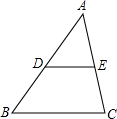 如图,若DE是△ABC的中位线,△ABC的周长为6,则△ADE的周长为( )
如图,若DE是△ABC的中位线,△ABC的周长为6,则△ADE的周长为( )| A、4 | B、3 | C、2 | D、1 |
分析:若DE是△ABC的中位线,所以DE等于BC的一半,且D、E分别是AB、AC的中点,则△ADE的周长可求.
解答:解:∵DE是△ABC的中位线,
∴AD=
AB,AE=
AC,DE=
BC.
∴△ADE的周长=
△ABC的周长=
×6=3.
故选B
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△ADE的周长=
| 1 |
| 2 |
| 1 |
| 2 |
故选B
点评:解决本题的关键是利用中点定义和中位线定理得到新三角形各边长与原三角形各边长的关系.

练习册系列答案
相关题目
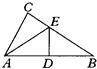 9、如图,若D是直角△ABC斜边上的中点,DE⊥AB,如果∠EAC:∠BAE=2:5,那么∠BAC=( )
9、如图,若D是直角△ABC斜边上的中点,DE⊥AB,如果∠EAC:∠BAE=2:5,那么∠BAC=( ) 如图,若D是AB中点,E是BC中点,
如图,若D是AB中点,E是BC中点, 如图,若O是△ABC内任意一点,点D,E,F分别在OA,OB,OC上,且DE∥AB,DF∥AC,AD:DO=1:2,
如图,若O是△ABC内任意一点,点D,E,F分别在OA,OB,OC上,且DE∥AB,DF∥AC,AD:DO=1:2, 如图,若D是AB中点,E是BC中点,
如图,若D是AB中点,E是BC中点,